
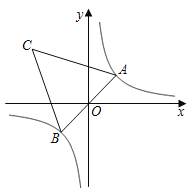
【题目】如图,在反比例函数![]() 的图象上有一动点
的图象上有一动点![]() ,连接
,连接![]() 并延长交图象的另一支于点
并延长交图象的另一支于点![]() ,在第二象限内有一点
,在第二象限内有一点![]() ,满足
,满足![]() ,当点
,当点![]() 运动时,点
运动时,点![]() 始终在函数
始终在函数![]() 的图象上运动,若
的图象上运动,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
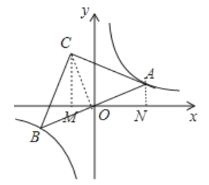
根据题意连接OC,作CM⊥x轴于M,AN⊥x轴于N,如图,利用反比例函数的性质得OA=OB,根据等腰三角形的性质得OC⊥AB,利用正切的定义得到![]() ,再证明Rt△OCM∽Rt△OAN,利用相似的性质得
,再证明Rt△OCM∽Rt△OAN,利用相似的性质得![]() ,然后根据k的几何意义即可求k的值.
,然后根据k的几何意义即可求k的值.
解:连接OC,作CM⊥x轴于M,AN⊥x轴于N,如图,
∵A、B两点为反比例函数与正比例函数的两交点,
∴点A、点B关于原点对称,
∴OA=OB,
∵CA=CB,
∴OC⊥AB,
在Rt△AOC中,tan∠CAO=![]() ,
,
∵∠COM+∠AON=90°,∠AON+∠OAN=90°,
∴∠COM=∠OAN,
∴Rt△OCM∽Rt△OAN,
∴![]() ,
,
而![]() ,
,
∴S△CMO=6,
∵![]() |k|=6,而k<0,
|k|=6,而k<0,
∴k=-12.
故选:A.


科目:初中数学 来源: 题型:
【题目】学以致用:问题1:怎样用长为![]() 的铁丝围成一个面积最大的矩形?
的铁丝围成一个面积最大的矩形?
小学时我们就知道结论:围成正方形时面积最大,即围成边长为![]() 的正方形时面积最大为
的正方形时面积最大为![]() .请用你所学的二次函数的知识解释原因.
.请用你所学的二次函数的知识解释原因.
思考验证:问题2:怎样用铁丝围一个面积为![]() 且周长最小的矩形?
且周长最小的矩形?
小明猜测:围成正方形时周长最小.
为了说明其中的道理,小明翻阅书籍,找到下面的结论:
在![]() 、
、![]() 均为正实数)中,若
均为正实数)中,若![]() 为定值
为定值![]() ,则
,则![]() ,只有当
,只有当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
思考验证:证明:![]() 、
、![]() 均为正实数)
均为正实数)
请完成小明的证明过程:
证明:对于任意正实数![]() 、
、![]()
![]()
![]()
![]()
解决问题:
(1)若![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”
” ![]() ;
;
(2)运用上述结论证明小明对问题2的猜测;
(3)填空:当![]() 时,
时,![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的半径为
的半径为![]() ,点
,点![]() 与圆心
与圆心![]() 不重合,给出如下定义:若在
不重合,给出如下定义:若在![]() 上存在一点
上存在一点![]() ,使
,使![]() ,则称点
,则称点![]() 为
为![]() 的特征点.
的特征点.
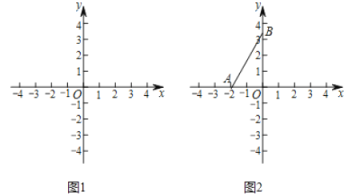
(1)当![]() 的半径为1时,如图1.
的半径为1时,如图1.
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的特征点是__________.
的特征点是__________.
②点![]() 在直线
在直线![]() 上,若点
上,若点![]() 为
为![]() 的特征点,求
的特征点,求![]() 的取值范围.
的取值范围.
(2)如图2,![]() 的圆心在
的圆心在![]() 轴上,半径为2,点
轴上,半径为2,点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的特征点,直接写出圆心
的特征点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,回答下列问题:
若m>0,只有当m= 时,![]() 有最小值 .
有最小值 .
思考验证:如图1,AB为半圆O的直径,C为半圆上任意一点(与点A、B不重合),过点C作CD⊥AB,垂足为D,AD=a,DB=b.
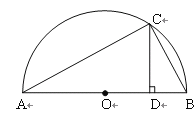
试根据图形验证![]() ≥
≥![]() ,并指出等号成立时的条件.
,并指出等号成立时的条件.
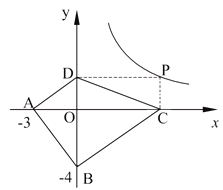
探索应用:如图2,已知A(-3,0),B(0,-4),P为双曲线![]() (x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
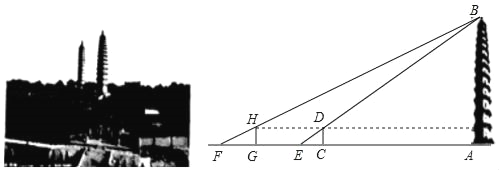
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
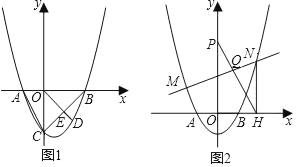
【题目】如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A、B两点(A在B左边),与y轴交于点C.连接AC、BC,D为抛物线上一动点(D在B、C两点之间),OD交BC于E点.
(1)若△ABC的面积为8,求m的值;
(2)在(1)的条件下,求![]() 的最大值;
的最大值;
(3)如图2,直线y=kx+b与抛物线交于M、N两点(M不与A重合,M在N左边),连MA,作NH⊥x轴于H,过点H作HP∥MA交y轴于点P,PH交MN于点Q,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com