
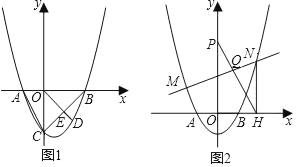
【题目】如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A、B两点(A在B左边),与y轴交于点C.连接AC、BC,D为抛物线上一动点(D在B、C两点之间),OD交BC于E点.
(1)若△ABC的面积为8,求m的值;
(2)在(1)的条件下,求![]() 的最大值;
的最大值;
(3)如图2,直线y=kx+b与抛物线交于M、N两点(M不与A重合,M在N左边),连MA,作NH⊥x轴于H,过点H作HP∥MA交y轴于点P,PH交MN于点Q,求点Q的横坐标.
【答案】(1)m=2;(2)![]() ;(3) Q点的横坐标为2.
;(3) Q点的横坐标为2.
【解析】
(1)解方程x2+(m-2)x一2m=0求出抛物线与x轴的交点,再令x=0,求出抛物线与y轴的交点,然后根据△ABC的面积为8,列方程求解即可;
(2)过点D作DF∥y轴交BC于F,求出点B、点C的坐标,用待定系数法求出直线BC的解析式,表示出DF的长,利用平行线分线段成比例定理列出关于![]() 的函数关系式,利用二次函数的性质即可求出结论;
的函数关系式,利用二次函数的性质即可求出结论;
(3)设M(x1,kx1+b)、N(x2,kx2+b),联立一次函数与二次函数关系式,整理可得x1+x2=2+k-m,x1x2=-2m-b. 过点M作MK⊥x轴于K,过点Q作QL⊥x轴于L,由△MKA∽△QLH,列比利式整理可得(km-b)(n-2)=0,然后分两种情况讨论可得点Q的横坐标.
(1) y=x2+(m-2)x-2m=(x+m)(x-2),
令y=0,则(x+m)(x-2)=0,解得x1=-m,x2=2,
∴A(-m,0)、B(2,0),
令x=0,则y=-2m,
∴C(0,-2m),
∴AB=2+m,OC=2m.
∵S△ABC=![]() ×(2+m)×2m=8,
×(2+m)×2m=8,
解得m1=2,m2=-4,
∵m>0,
∴m=2;
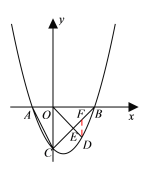
(2) 过点D作DF∥y轴交BC于F,
由(1)可知:m=2,
∴抛物线的解析式为y=x2-4,
∴B(2,0)、C(0,-4),
∴直线BC的解析式为y=2x-4.
设D(t,t2-4),则F(t,2t-4),
∴DF=2t-4-(t2-4)=-t2+2t,OC=4,
∵DF∥y轴,
∴![]() =
=![]() =
=![]() =-
=-![]() (t-1)2+
(t-1)2+![]() ,
,
当t=1时,有最大值为
![]() ,此时D(1,3);
,此时D(1,3);
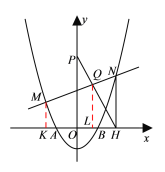
(3) 设M(x1,kx1+b)、N(x2,kx2+b),
联立 ,整理得x2+(m-2-k)x-2m-b=0,
,整理得x2+(m-2-k)x-2m-b=0,
∴x1+x2=2+k-m,x1x2=-2m-b,
设点Q的横坐标为n,则Q(n,kn+b),
过点M作MK⊥x轴于K,过点Q作QL⊥x轴于L,
∵MA∥PH,
∴△MKA∽△QLH,
∴![]() =
=![]() ,
,
即![]() ,整理得kx1x2+b(x1+x2)+kmn+bm-bn=0,
,整理得kx1x2+b(x1+x2)+kmn+bm-bn=0,
∴k(-2m-b)+b(2+k-m)+kmn+bm-bn=0,
∴(km-b)(n-2)=0,
②km-b=0,此时直线为y=k(x+m),过点A(-m,0),不符合题意,
②当n-2=0,此时n=2,Q点的横坐标为2.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】某校九年级(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计如表所示:
自选项目 | 人数 | 频率 |
立定跳远 | b | 0.18 |
三级蛙跳 | 12 | 0.24 |
一分钟跳绳 | 8 | a |
投掷实心球 | 16 | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若该校九年级共有400名学生,试估计年级选择“一分钟跳绳”项目的总人数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至少有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
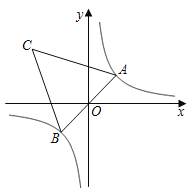
【题目】如图,在反比例函数![]() 的图象上有一动点
的图象上有一动点![]() ,连接
,连接![]() 并延长交图象的另一支于点
并延长交图象的另一支于点![]() ,在第二象限内有一点
,在第二象限内有一点![]() ,满足
,满足![]() ,当点
,当点![]() 运动时,点
运动时,点![]() 始终在函数
始终在函数![]() 的图象上运动,若
的图象上运动,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

查看答案和解析>>
科目:初中数学 来源: 题型:
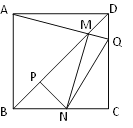
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D,E分别是边AB,AC上的点,DE∥BC,点H是边BC上的点,连接AH交线段DE于点G,且BH=DE=12,DG=8,S△ADG=12,则S四边形BCED=( )

A.24B.22.5C.20D.25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com