练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

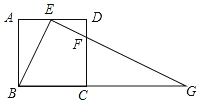
    【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DC=4DF，连接EF并延长交BC的延长线于点G．

    （1）求证：△ABE∽△DEF；

    （2）若正方形的边长为16，求BG的长．

    【答案】（1）证明见解析；（2）40

    【解析】

    （1）根据两组对应边的比相等且夹角对应相等的两个三角形相似进行求证；

    （2）通过证明△DEF∽△CGF得出=，求出CG的长即可．

    （1）证明：∵ABCD为正方形，

    ∴AD=AB=DC=BC，∠A=∠D=90°，

    ∵AE=ED，

    ∴=，

    ∵DC=4DF，

    ∴=，

    ∴=，

    ∴△ABE∽△DEF；

    （2）∵ABCD为正方形，

    ∴ED∥BG，

    ∴△DEF∽△CGF，

    ∴=，

    又∵DC=4DF，正方形的边长为16，

    ∴ED=8，CG=24，

    ∴BG=BC+CG=40．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，王老师将某班近三个月跳跃类项目的训练情况做了统计，并绘制了折线统计图，则根据图中信息以下判断错误的是（ ）

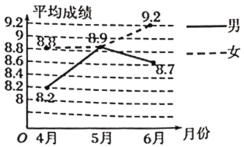
    A.男女生5月份的平均成绩一样

    B.4月到6月，女生平均成绩一直在进步

    C.4月到5月，女生平均成绩的增长率约为

    D.5月到6月女生平均成绩比4月到5月的平均成绩增长快

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了发展乡村旅游，建设美丽乡村，某中学七年级（1）班同学都积极参加了植树活动，将今年三月份该班同学的植树情况绘制成如图所示的不完整的统计图．已知植树量为2株的人数占总人数的32%．

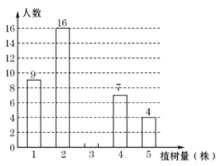
    （1）该班的总人数为____________，植树株数的众数是____________，植树株数的中位数是____________；

    （2）请将条形统计图补充完整；

    （3）若将该班同学的植树情况绘制成扇形统计图，求“植树量为3株”所对应的扇形的园心角度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

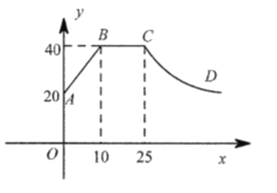
    【题目】一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x(min)的变化规律如图所示(其中分别为线段，为双曲线的一部分)：

    （1）上课后第与第相比较，何时学生注意力更集中？

    （2）某道难题需连续讲，为保证效果，学生注意力指数不宜低于，老师能否在所需要求下讲完这道题？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

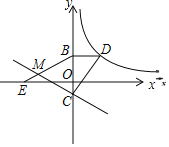
    【题目】如图，已知点D在反比例函数的图象上，过点D作x轴的平行线交y轴于点B（0，2），过点A(,0)的直线y＝kx+b与y轴于点C，且BD＝2OC，tan∠OAC＝．

    （1）求反比例函数的解析式；

    （2）连接CD，试判断线段AC与线段CD的关系，并说明理由；

    （3）点E为x轴上点A左侧的一点，且AE＝BD，连接BE交直线CA于点M，求tan∠BMC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

    （1）证明与推断：

    ①求证：四边形CEGF是正方形；

    ②推断：的值为　 　：

    （2）探究与证明：

    将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

    （3）拓展与运用：

    正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：对于任意正实数a、b，∵≥0，　∴≥0，

    ∴≥，只有当a＝b时，等号成立．

    结论：在≥（a、b均为正实数）中，若ab为定值p，则a+b≥，只有当a＝b时，a+b有最小值．

    根据上述内容，回答下列问题：

    若m＞0，只有当m＝ 时，有最小值 ．

    思考验证：如图1，AB为半圆O的直径，C为半圆上任意一点（与点A、B不重合），过点C作CD⊥AB，垂足为D，AD＝a，DB＝b．

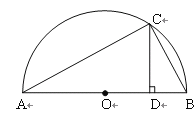
    试根据图形验证≥，并指出等号成立时的条件．

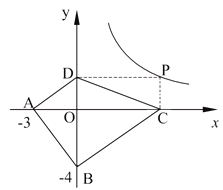
    探索应用：如图2，已知A(－3，0)，B(0，－4)，P为双曲线（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

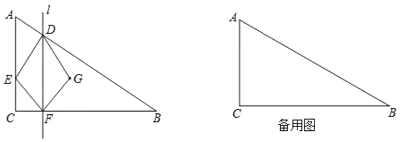
    【题目】如图，中，，点、同时从点出发，以的速度分别沿、匀速运动，当点到达点时，两点同时停止运动，设运动时间为．过点作的垂线交于点，点与点关于直线对称．

    （1）当_____时，点在的平分线上；

    （2）当_____时，点在边上；

    （3）设与重合部分的面积为，求与之间的函数关系式，并写的取值范围．

    查看答案和解析>>

    同步练习册答案