
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以
出发,以![]() 的速度分别沿
的速度分别沿![]() 、
、![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() .过点
.过点![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
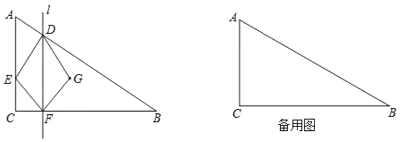
(1)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 边上;
边上;
(3)设![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写
之间的函数关系式,并写![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
【解析】
(1)过点![]() 做
做![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,所以
出发,所以![]() ,且
,且![]() 也是
也是![]() 的角平分线,由
的角平分线,由![]() 得:
得:![]() ,
,![]()
![]() ,
,![]() ,可求得
,可求得![]() 、
、![]() 的长度,由
的长度,由![]() ,
,![]() ,构造关于
,构造关于![]() 的方程可以求得答案.
的方程可以求得答案.
(2)点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由(1)中的数值,结合
,由(1)中的数值,结合![]() ,构造出关于
,构造出关于![]() 的方程,可以得到答案.
的方程,可以得到答案.
(3)由![]() 得到
得到![]() ,
,![]()
![]() ,即
,即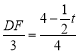 ,得到
,得到![]() ,分两种情况讨论:
,分两种情况讨论:
①当![]() 时,
时,![]() ;
;
②当![]() 时,设
时,设![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,求得
,求得![]() ,解出
,解出![]() 与
与![]() 的关系,继而求得
的关系,继而求得![]() 与
与![]() 的关系.
的关系.
解:(1)![]()
设![]() ,
,![]() 相交于
相交于![]() ,过点
,过点![]() 做
做![]() ,垂足为
,垂足为![]() ,
,![]() ,
,
垂足为![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,所以四边形
出发,所以四边形![]() 、四边形
、四边形![]() 都是正方形,
都是正方形,
![]() ,
,
又![]() 也是
也是![]() 的角平分线,
的角平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,又
,又![]() ,
,
![]()
![]() ,解得:
,解得:![]() .
.

(2)![]()
点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
所以![]() ,
,
![]()
![]() ,
,
即: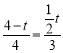 ,
,
解得:![]() .
.
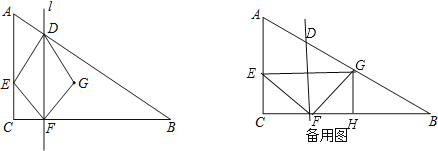
(3)![]() ,
,
![]() ,
,
![]()
![]() ,
,
即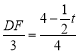 ,
,
解得![]()
①当![]() 时,
时,![]() .
.
②当![]() 时,设
时,设![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,
,
则![]() ,
,
![]()
![]() ,
,
解得![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
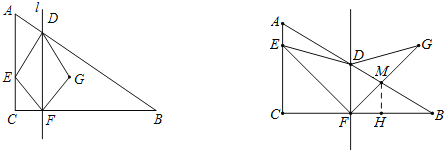
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DC=4DF,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为16,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
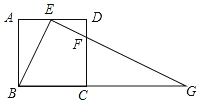
【题目】等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.
(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?
(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?
(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=![]() x2+bx+3的对称轴为直线x=
x2+bx+3的对称轴为直线x=![]() 1.若关于x的一元二次方程
1.若关于x的一元二次方程![]() x2+bx+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
x2+bx+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
A.![]() 12<t≤3B.
12<t≤3B.![]() 12<t<4C.
12<t<4C.![]() 12<t≤4D.
12<t≤4D.![]() 12<t<3
12<t<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如我们把函数![]() 沿
沿![]() 轴翻折得到函数
轴翻折得到函数![]() ,函数
,函数![]() 与函数
与函数![]() 的图象合起来组成函数
的图象合起来组成函数![]() 的图象.若直线
的图象.若直线![]() 与函数
与函数![]() 的图象刚好有两个交点,则满足条件的
的图象刚好有两个交点,则满足条件的![]() 的值可以为_______________(填出一个合理的值即可).
的值可以为_______________(填出一个合理的值即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
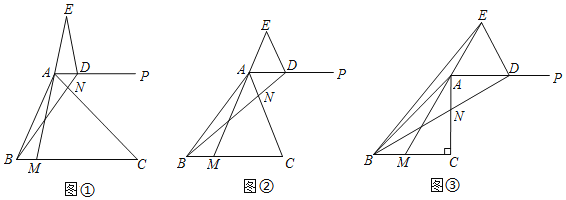
【题目】在△ABC中,CA=CB,0°<∠C≤90°.过点A作射线AP∥BC,点M、N分别在边BC、AC上(点M、N不与所在线段端点重合),且BM=AN,连结BN并延长交AP于点D,连结MA并延长交AD的垂直平分线于点E,连结ED.
(猜想)如图①,当∠C=45°时,可证△BCN≌△ACM,从而得出∠CBN=∠CAM,进而得出∠BDE的大小为 度.
(探究)如图②,若∠C=α.
(1)求证:△BCN≌△ACM.
(2)∠BDE的大小为 度(用含a的代数式表示).
(应用)如图③,当∠C=90°时,连结BE.若BC=3,∠BAM=15°,则△BDE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com