
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
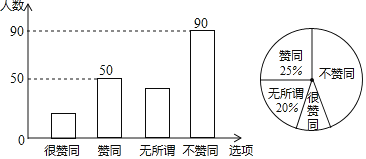
(1)本次共调查了 名家长;扇形统计图中“很赞同”所对应的圆心角是 度.已知该校共有1600名家长,则“不赞同”的家长约有 名;请补全条形统计图;
(2)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
【答案】(1)200,36,720,见解析;(2)列表法见解析,![]()
【解析】
(1)从两个统计图可得,“赞同”的有50名,占调查总人数的25%,可求出调查总人数;进而求出“无所谓”和“很赞同”的人数,很赞同的圆心角度数为360°的![]() ,样本估计总体,样本中“不赞同”的占
,样本估计总体,样本中“不赞同”的占![]() ,估计总体1600户的
,估计总体1600户的![]() 是“不赞同”的人数;即可补全条形统计图:
是“不赞同”的人数;即可补全条形统计图:
(2)用列表法或树状图法列举出所有等可能出现的情况,从中找出1男1女的情况数,进而求出概率.
解:(1)总人数:50÷25%=200名,无所谓人数:200×20%=40名,很赞同人数:200﹣90﹣50﹣40=20名,
很赞同对应圆心角:360°×![]() =36°,
=36°,
1600×![]() =720名,
=720名,
故答案为:200,36,720,补全条形统计图如图所示:
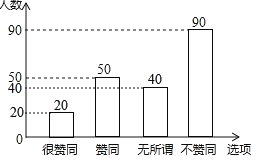
(2)用列表法表示所有可能出现的情况如下:
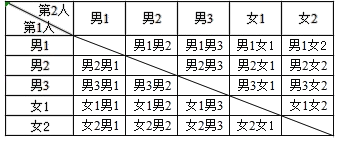
共有20种可能出现的情况,正确“1男1女”的有12种,
∴P(1男1女)=![]() ,
,
答:选中“1男1女”的概率为![]() .
.


科目:初中数学 来源: 题型:
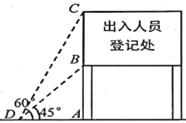
【题目】2020年春节期间,昆明市政府为了进一步做好新冠肺炎疫情的防控工作,在各个高速公路出入口均设立检测点,对出入人员进行登记和体温检测,下图为一高速路口检测点的指示牌,已知立杆![]() 的高度是
的高度是![]() ,从侧面
,从侧面![]() 点处测得指示牌
点处测得指示牌![]() 点和
点和![]() 点的仰角分别是
点的仰角分别是![]() 和
和![]() ,求
,求![]() 的长.(结果精确到
的长.(结果精确到![]() .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=ax2﹣2ax﹣3a(a≠0)和点A(0,﹣3),将点A向右平移2个单位,再向上平移5个单位,得到点B.
(1)求点B的坐标;
(2)求抛物线C1的对称轴;
(3)把抛物线C1沿x轴翻折,得到一条新抛物线C2,抛物线C2与抛物线C1组成的图象记为G,若图象G与线段AB恰有一个交点时,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
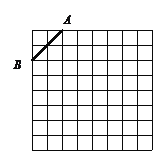
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标和△ABC的周长(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△DEC,连结AE和BD,试说明四边形ABDE是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,连接
中,连接![]() 点
点![]() 为
为![]() 上一点,使得
上一点,使得![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
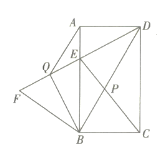
(1)求证:![]() .
.
(2)若![]() 求
求![]() 的长.
的长.
(3)在(2)的条件下,将![]() 沿着
沿着![]() 对折得到
对折得到![]() 点
点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 试求
试求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张半径为![]() 的圆形纸片,点
的圆形纸片,点![]() 为圆心,将该圆形纸片沿直线
为圆心,将该圆形纸片沿直线![]() 折叠,直线
折叠,直线![]() 交
交![]() 于
于![]() 两点.
两点.
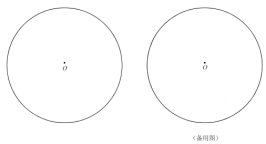
(1)若折叠后的圆弧恰好经过点![]() ,利用直尺和圆规在图中作出满足条件的一条直线
,利用直尺和圆规在图中作出满足条件的一条直线![]() (不写作法,保留作图痕迹),并求此时线段
(不写作法,保留作图痕迹),并求此时线段![]() 的长度.
的长度.
(2)已知![]() 是
是![]() 一点,
一点,![]() .
.
①若折叠后的圆弧经过点![]() ,则线段
,则线段![]() 长度的取值范围是________.
长度的取值范围是________.
②若折叠后的圆弧与直线![]() 相切于点
相切于点![]() ,则线段
,则线段![]() 的长度为_________
的长度为_________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜市场为指导某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供的信息如下:
信息1:售价和月份满足一次函数关系,如下表所示.
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2:成本和月份满足二次函数关系,并且知道该种蔬菜在6月成本达到最低为1元/千克,9月成本为4元/千克.
根据以上信息回答下列问题:
(1)在7月,这种蔬菜的成本是多少元每千克?
(2)在过去的一年中,某商家平均每天卖出![]() 该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com