
【题目】(1)问题发现如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为______;②
的值为______;②![]() 的度数为______.
的度数为______.
(2)类比探究如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(3)拓展延伸在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 在同一条直线上时
在同一条直线上时![]() 的长.
的长.

【答案】(1)①1;②![]() ;(2)
;(2)![]() ,
,![]() .理由见解析;(3)2或4.
.理由见解析;(3)2或4.
【解析】
(1)①证明△COA≌△DOB(SAS),得AC=BD,比值为1;
②由△COA≌△DOB,得∠CAO=∠DBO,然后根据三角形的内角和定理先求∠OAB+∠OBA的值,再求∠AMB的值即可;
(2)根据锐角三角比可得![]() ,根据两边的比相等且夹角相等可得△AOC∽△BOD,根据相似撒尿性的性质求解即可;
,根据两边的比相等且夹角相等可得△AOC∽△BOD,根据相似撒尿性的性质求解即可;
(3)当点![]() 与点
与点![]() 在同一条直线上,有两种情况:如图3和图4,然后根据旋转的性质和勾股定理,可得AD的长.
在同一条直线上,有两种情况:如图3和图4,然后根据旋转的性质和勾股定理,可得AD的长.
(1)①∵![]() ,
,
∴∠BOD=∠AOC,
又∵![]() ,
,![]() ,
,
∴△BOD≌△AOC,
∴BD=AC,
∴![]() =1;
=1;
②∵![]() ,
,
∴∠OAB+∠OBA=140°,
∵△BOD≌△AOC,
∴∠CAO=∠DBO,
∴∠CAO+∠OAB+∠ABM=∠DBO+∠OAB+∠ABM=∠OAB+∠OBA=140°,
∴∠AMB=![]() ;
;
(2)如图2,
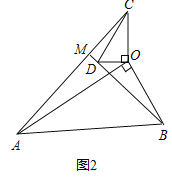
![]() ,
,![]() .理由如下:
.理由如下:
![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
同理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,∠CAO=∠DBO,
,∠CAO=∠DBO,
∵∠BEO+∠DBO=90°,
∴∠CAE+∠AEM=90°,
∴∠AMB=90°;
(3) ∵∠A=30°,![]() ,
,
∴OA=![]() =3.
=3.
如图3,当点D和点A在点O的同侧时,
∵![]() ,
,
∴AD=3-2=2;
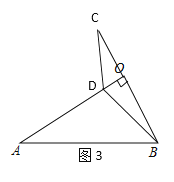
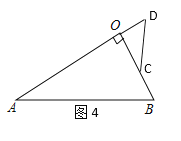
如图4,当点D和点A在点O的两侧时,
∵![]() ,,OA=3
,,OA=3
∴AD=3+1=4.
综上可知,AD的长是2或4.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
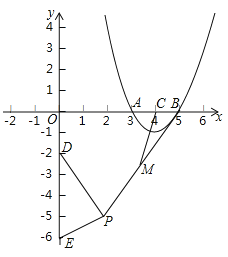
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
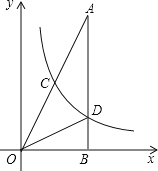
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象分别交
在第一象限内的图象分别交![]() ,
,![]() 于点
于点![]() 和点
和点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求反比例函数解析式;
(3)求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
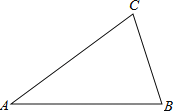
【题目】如图,已知△ABC.
(1)实践与操作:
利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作BC边上的高AD;
②作△ABC的角平分线BE;
(2)综合与运用;
若△ABC中,AB=AC且∠CAB=36°,
请根据作图和已知写出符合括号内要求的正确结论;
结论1: ;(关于角)
结论2: ;(关于线段)
结论3: .(关于三角形)
查看答案和解析>>
科目:初中数学 来源: 题型:
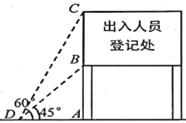
【题目】2020年春节期间,昆明市政府为了进一步做好新冠肺炎疫情的防控工作,在各个高速公路出入口均设立检测点,对出入人员进行登记和体温检测,下图为一高速路口检测点的指示牌,已知立杆![]() 的高度是
的高度是![]() ,从侧面
,从侧面![]() 点处测得指示牌
点处测得指示牌![]() 点和
点和![]() 点的仰角分别是
点的仰角分别是![]() 和
和![]() ,求
,求![]() 的长.(结果精确到
的长.(结果精确到![]() .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要进一批鸡蛋进行销售,有![]() 、
、![]() 两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
(1)下列抽样方式比较合理的是哪一种?请简述原因.
①分别从![]() 、
、![]() 两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
②分别从![]() 、
、![]() 两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量(单位:![]() ),结果如表所示(数据包括左端点不包括右端点).
),结果如表所示(数据包括左端点不包括右端点).
45~47 | 47~49 | 49~51 | 51~53 | 53~55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果从这两家农场提供的鸡蛋中随机拿一个,分别估计两家鸡蛋质量在![]() (单位:
(单位:![]() )范围内的概率(数据包括左端点不包括右端点);
)范围内的概率(数据包括左端点不包括右端点);
②如果你是超市经营者,试通过数据分析确定选择哪家农场提供的鸡蛋.
查看答案和解析>>
科目:初中数学 来源: 题型:
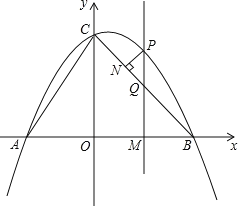
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求此抛物线的表达式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .试探究点P在运动过程中,是否存在这样的点
.试探究点P在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .请用含
.请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出当
的长,并求出当![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
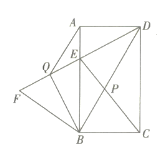
【题目】如图,在矩形![]() 中,连接
中,连接![]() 点
点![]() 为
为![]() 上一点,使得
上一点,使得![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() 求
求![]() 的长.
的长.
(3)在(2)的条件下,将![]() 沿着
沿着![]() 对折得到
对折得到![]() 点
点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 试求
试求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com