
【题目】如图,已知△ABC.
(1)实践与操作:
利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作BC边上的高AD;
②作△ABC的角平分线BE;
(2)综合与运用;
若△ABC中,AB=AC且∠CAB=36°,
请根据作图和已知写出符合括号内要求的正确结论;
结论1: ;(关于角)
结论2: ;(关于线段)
结论3: .(关于三角形)
【答案】(1)①②如图,见解析;(2)∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).
【解析】
(1)①按照过直线外一点作直线的垂线步骤作即可;②按照作一个角的平分线的作法来做即可.
(2)根据等腰三角形的判定与性质结合(1)中的图形即可求解.
(1)①②如图:
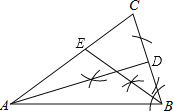
(2)∵AB=AC且∠CAB=36°,
∴∠ABC=∠C=72°,
∵BE是△ABC的角平分线,
∴∠ABE=∠CBE=36°,
∴∠ABE=∠CBE=∠CAB=36°.
∵AD是BC边上的高,AB=AC,
∴BD=DC,∠BAD=∠CAD.
∵∠EAB=∠ABE=36°,∠C=∠CEB=72°,
∴AE=BE,BC=BE,
∴△ABE,△BCE都是等腰三角形.
则结论1:∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);
结论2:BD=DC,AE=BE,BC=BE(关于线段);
结论3:△ABE,△BCE都是等腰三角形(关于三角形).
故答案为∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】小宇设计了一个随机碰撞模拟器:在模拟器中有![]() ,
,![]() ,
,![]() 三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个
三种型号的小球,它们随机运动,当两个小球相遇时会发生碰撞(不考虑多个小球相撞的情况).若相同型号的两个小球发生碰撞,会变成一个![]() 型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个
型小球;若不同型号的两个小球发生碰撞,则会变成另外一种型号的小球,例如,一个![]() 型小球和一个
型小球和一个![]() 型小球发生碰撞,会变成一个
型小球发生碰撞,会变成一个![]() 型小球.现在模拟器中有
型小球.现在模拟器中有![]() 型小球12个,
型小球12个,![]() 型小球9个,
型小球9个,![]() 型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
型小球10个,如果经过各种两两碰撞后,最后只剩一个小球.以下说法:
①最后剩下的小球可能是![]() 型小球;
型小球;
②最后剩下的小球一定是![]() 型小球;
型小球;
③最后剩下的小球一定不是![]() 型小球.
型小球.
其中正确的说法是:( )
A.①B.②③C.③D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
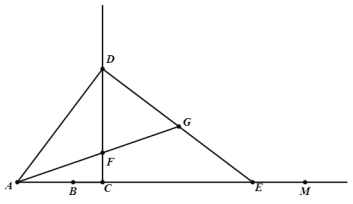
【题目】如图,射线AM上有一点B,AB=6.点C是射线AM上异于B的一点,过C作CD⊥AM,且CD=![]() AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
AC.过D点作DE⊥AD,交射线AM于E. 在射线CD取点F,使得CF=CB,连接AF并延长,交DE于点G.设AC=3x.
(1) 当C在B点右侧时,求AD、DF的长.(用关于x的代数式表示)
(2)当x为何值时,△AFD是等腰三角形.
(3)若将△DFG沿FG翻折,恰使点D对应点![]() 落在射线AM上,连接
落在射线AM上,连接![]() ,
,![]() .此时x的值为 (直接写出答案)
.此时x的值为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=2AC,点A(2,0)、B(0,4),点C在第一象限内,双曲线y=![]() (x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.
(x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
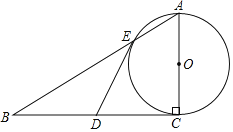
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为______;②
的值为______;②![]() 的度数为______.
的度数为______.
(2)类比探究如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请判断
.请判断![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
(3)拓展延伸在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 在同一条直线上时
在同一条直线上时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
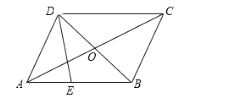
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE = 2AE.设![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果点F是线段OC的中点,那么向量![]() ,并在图中画出向量
,并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本题结果用向量![]() 的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,李林和王聪两人在玩转盘游戏时,分别把转盘![]() ,
,![]() 分成3等份和4等份,并标上数字(如图所示).游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个数字之和小于4,则李林获胜;若数字之和大于4,则王聪获胜,如果指针落在分割线上,则需要重新转动转盘.
分成3等份和4等份,并标上数字(如图所示).游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个数字之和小于4,则李林获胜;若数字之和大于4,则王聪获胜,如果指针落在分割线上,则需要重新转动转盘.
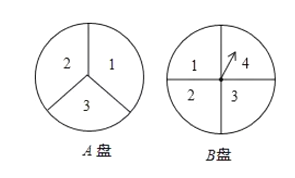
(1)用列表法或画树状图法中的一种方法,求所有可能出现的结果.
(2)该游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com