
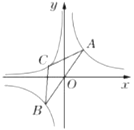
【题目】如图,点![]() ,
,![]() 是双曲线
是双曲线![]() 图象上的两点,连接
图象上的两点,连接![]() ,线段
,线段![]() 经过点
经过点![]() ,点
,点![]() 为双曲线
为双曲线![]() 在第二象限的分支上一点,当
在第二象限的分支上一点,当![]() 满足
满足![]() 且
且![]() 时,
时,![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出![]() ,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出
,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出![]() =
=![]() ,因为S△AOE=9,可得S△COF=
,因为S△AOE=9,可得S△COF=![]() ,再根据反比例函数的几何意义即可解决问题.
,再根据反比例函数的几何意义即可解决问题.
解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.

∵A、B关于原点对称,
∴OA=OB,
∵AC=BC,OA=OB,
∴OC⊥AB,
∴∠CFO=∠COA=∠AEO=90°,
∴∠COF+∠AOE=90°,∠AOE+∠EAO=90°,
∴∠COF=∠OAE,
∴△CFO∽△OEA,
∴![]() ,
,
∵CA:AB=13:24,AO=OB,
∴CA:OA=13:12,
∴CO:OA=5:12,
∴![]() =
=![]() ,
,
∵S△AOE=9,
∴S△COF=![]() ,
,
∴![]() ,
,
∵k<0,
∴![]()
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,![]() ,连结
,连结![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点.
的中点.
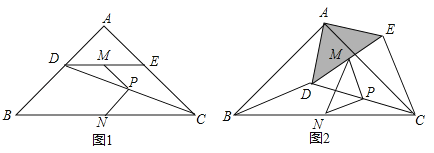
(1)观察猜想图1中,线段![]() 与
与![]() 的数量关系是_______,位置关系是_______;
的数量关系是_______,位置关系是_______;
(2)探究证明把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,连结
逆时针方向旋转到图2的位置,连结![]() 、
、![]() 、
、![]() ,判断
,判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)拓展延伸把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
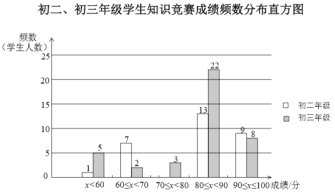
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接2022年的冬奥会,中小学都积极开展冰上运动,小乙和小丁进行500米短道速滑比赛,他们的五次成绩(单位:秒)如表所示:
1 | 2 | 3 | 4 | 5 | |
小乙 | 45 | 63 | 55 | 52 | 60 |
小丁 | 51 | 53 | 58 | 56 | 57 |
设两人的五次成绩的平均数依次为![]() 乙,
乙,![]() 丁,成绩的方差一次为
丁,成绩的方差一次为![]() ,
,![]() ,则下列判断中正确的是( )
,则下列判断中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
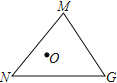
【题目】问题背景:如图,将![]() 绕点
绕点![]() 逆时针旋转60°得到
逆时针旋转60°得到![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,可推出结论:
,可推出结论:![]()
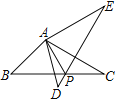
问题解决:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 是
是![]() 内一点,则点
内一点,则点![]() 到
到![]() 三个顶点的距离和的最小值是___________
三个顶点的距离和的最小值是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
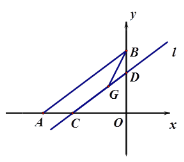
【题目】如图,已知A(-4,0)、B(0,3),一次函数![]() 与坐标轴分别交于C、D两点,G为CD上一点,且DG:CG=1:2,连接BG,当BG平分∠ABO时,则b的值为____.
与坐标轴分别交于C、D两点,G为CD上一点,且DG:CG=1:2,连接BG,当BG平分∠ABO时,则b的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
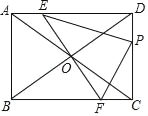
【题目】如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).
(1)填空:PC= ,FC= ;(用含x的代数式表示)
(2)求△PEF面积的最小值;
(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁两位同学做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人,则第二次传球后球回到甲手里的概率是________;第三次传球后球回到甲手里的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com