
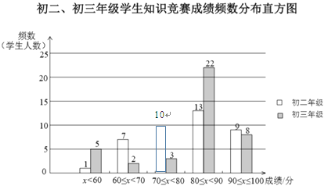
【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
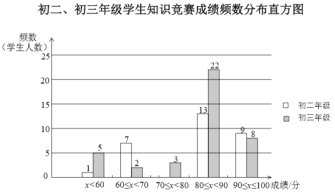
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学生,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.
【答案】(1)见详解;(2)80.5;(3)初二;初二年级前40%的最低成绩为84,未超过初三年级的学生成绩的中位数86;(4)225.
【解析】
(1)根据初二年级抽取的总人数减去已知的各段人数即得;
(2)根据中位数的定义,将所有数据从小到大的顺序排列取中间两数的平均值即得;
(3)利用中位数所表示的意义即得;
(4)将初二优秀人数所占百分比与总人数相乘即得.
(1)如下图:
(2)∵初二共抽取40名学生成绩
∴中位数为从小到大排列的数据的第20位和第21位的平均值
∴根据分布直方图可知数据的第20位和第21位是知识竞赛成绩在![]() 这一组的数据从小到大排列的第2位和第3位:80、81
这一组的数据从小到大排列的第2位和第3位:80、81
∴![]()
故答案为:80.5.
(3)∵初二年级的学生成绩的前40%为所有40个数据从小到大排列的最后16个数据,这16个数据中的最小数据为:84,且初三年级的学生成绩的中位数是:86.
∴84分在初三年级学生成绩中未进前50%
∴![]() 同学是初二年级
同学是初二年级
故答案为:初二;初二年级前40%的最低成绩为84,未超过初三年级的学生成绩的中位数86.
(4)∵初二年级学生成绩85分及以上的人数的百分比为:![]()
∴估计初二年级竞赛成绩优秀的人数为![]() (名)
(名)
故答案为:225.


科目:初中数学 来源: 题型:
【题目】《中国汉字听写大会》 唤醒了很多人对文字基本功的重视和对汉字文化的学习,某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列统计图表:
取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩 |
A组 |
|
B组 |
|
C组 |
|
D组 |
|
E组 |
|

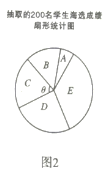
请根据所给信息,解答下列问题
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,表示![]() 组扇形的圆心角
组扇形的圆心角![]() 的度数为_______度;
的度数为_______度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人;
(4)经过统计发现,在![]() 组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺市某校想知道学生对“遥远的赫图阿拉”,“旗袍故里”等家乡旅游品牌的了解程度,随机抽取了部分学生进行问卷调查,问卷有四个选项(每位被调查的学生必选且只选一项)A.十分了解,B.了解较多,C.了解较少,D.不知道.将调查的结果绘制成如下两幅不完整的统计图,请根据两幅统计图中的信息回答下列问题:
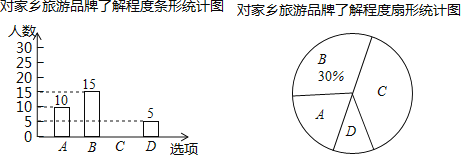
(1)本次调查了多少名学生?
(2)补全条形统计图;
(3)该校共有500名学生,请你估计“十分了解”的学生有多少名?
(4)在被调查“十分了解”的学生中有四名学生会干部,他们中有3名男生和1名女生,学校想从这4人中任选两人做家乡旅游品牌宣传员,请用列表或画树状图法求出被选中的两人恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,
,![]() 上的点(不与端点重合).对于任意菱形
上的点(不与端点重合).对于任意菱形![]() ,下面四个结论中:①存在无数个四边形
,下面四个结论中:①存在无数个四边形![]() 是平行四边形;②存在无数个四边形
是平行四边形;②存在无数个四边形![]() 是菱形;③存在无数个四边形
是菱形;③存在无数个四边形![]() 是矩形;④存在无数个四边形
是矩形;④存在无数个四边形![]() 是正方形;所有正确结论的序号是______.
是正方形;所有正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合)将△BCP沿CP所在的直线翻折,得到![]() ,连接
,连接![]() ,下面有四个判断:
,下面有四个判断:
①当AP=BP时,![]() ∥CP;
∥CP;
②当AP=BP时,![]()
③当CP⊥AB时,![]() ;
;
④![]() 长度的最小值是1.
长度的最小值是1.
所有正确结论的序号是( )
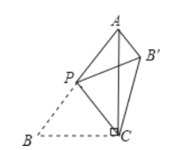
A.①③④B.①②C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号的电热水器工作过程如下:在接通电源以后,从初始温度20![]() 下加热水箱中的水,当水温达到设定温度60
下加热水箱中的水,当水温达到设定温度60![]() 时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30
时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30![]() 时,再次自动加热水箱中的水至60
时,再次自动加热水箱中的水至60![]() ,加热停止;当水箱中的水温下降到30
,加热停止;当水箱中的水温下降到30![]() 时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温
时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温![]() 是时间
是时间![]() 的函数,其中
的函数,其中![]() (单位:
(单位:![]() )表示水箱中水的温度,
)表示水箱中水的温度,![]() (单位:
(单位:![]() )表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
)表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
(1)小宇记录了从初始温度20![]() 第一次加热至设定温度60
第一次加热至设定温度60![]() ,之后水温冷却至保温温度30
,之后水温冷却至保温温度30![]() 的过程中,
的过程中,![]() 随
随![]() 的变化情况,如下表所示:
的变化情况,如下表所示:
接通电源后的时间 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | … |
水箱中水的温度 | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
①请写出一个符合加热阶段![]() 与
与![]() 关系的函数解析式______________;
关系的函数解析式______________;
②根据该电热水器的工作特点,当第二次加热至设定温度60![]() 时,距离接通电源的时间
时,距离接通电源的时间![]() 为________
为________![]() .
.
(2)根据上述的表格,小宇画出了当![]() 时的函数图象,请根据该电热水器的工作特点,帮他画出当
时的函数图象,请根据该电热水器的工作特点,帮他画出当![]() 时的函数图象.
时的函数图象.
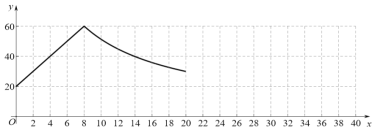
(3)已知适宜人体沐浴的水温约为![]() ,小宇在上午8点整接通电源,水箱中水温为20
,小宇在上午8点整接通电源,水箱中水温为20![]() ,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
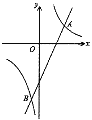
【题目】如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交点为
的图象交点为![]() ,
,![]() .
.
(1)求反比例函数与一次函数的解析式及![]() 点坐标;
点坐标;
(2)若![]() 是
是![]() 轴上的点,且满足
轴上的点,且满足![]() 的面积为10,求
的面积为10,求![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com