
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一动点(与点
边上一动点(与点![]() 不重合),连接
不重合),连接![]() 将
将![]() 的两边所在射线
的两边所在射线![]() 以点
以点![]() 为中心,顺时针旋转
为中心,顺时针旋转![]() 分别交射线
分别交射线![]() 于点
于点![]() .
.
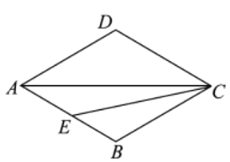
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示) ;
的式子表示) ;
(3)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)详情见解析;(2)∠AFC=α+30°;(3)AF+AE=![]() CG,证明见解析
CG,证明见解析
【解析】
(1)按照要求,利用旋转的性质得出对应点的位置,从而得出答案即可;
(2)利用旋转性质得出∠ECF=∠ACG=120°,由此进一步求出∠ACE=∠FCG=α,然后结合菱形的选择可知∠DAC=∠BAC=30°,据此进一步求出答案即可;
(3)作CH⊥AG于点H,首先证明△ACE与△GCF全等,由此进一步得出HG=CG×cos∠CGH,据此进一步求得AG=![]() CG,进而得出答案即可.
CG,进而得出答案即可.
(1)补全的图形如图所示:
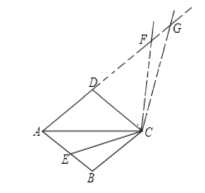
(2)由旋转性质可得:∠ECF=∠ACG=120°,
∴∠ACE+∠ACF=∠ACF+∠FCG,
∴∠ACE=∠FCG=α,
∵四边形ABCD为菱形,∠DAB=60°,
∴∠DAC=∠BAC=30°,
∴∠AGC=30°,
∴∠AFC=α+30°;
(3)线段![]() 与
与![]() 之间的数量关系为:AF+AE=
之间的数量关系为:AF+AE=![]() CG,证明如下:
CG,证明如下:
如图,作CH⊥AG于点H,
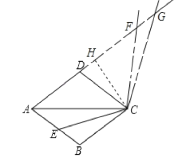
由(2)可得:∠BAC=∠DAC=∠AGC=30°,
∴CA=CG,
∴HG=![]() AG,
AG,
在△ACE与△GCF中,
∵∠ACE=∠GCF,CA=CG,∠CAE=∠CGF,
∴△ACE△GCF(ASA),
∴AE=FG,
在Rt△HCG中,
HG=CG×cos∠CGH=![]() CG,
CG,
∴AG=![]() CG,
CG,
即:AF+AE=AF+FG=AG=![]() CG,
CG,
∴线段![]() 与
与![]() 之间的数量关系为:AF+AE=
之间的数量关系为:AF+AE=![]() CG.
CG.


科目:初中数学 来源: 题型:
【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供3000名学生就餐;同时开放1个大餐厅,1个小餐厅,可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全校4500名学生就餐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=-x2+2bx+c与直线l:y=9x+14交于点A,其中点A的横坐标为-2.
(1)请用含有b的代数式表示c: ;
(2)若点B在直线l上,且B的横坐标为-1,点C的坐标为(b,5).
①若抛物线M还过点B,直接写出该抛物线的解析式;
②若抛物线M与线段BC恰有一个交点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G经过点
的图象G经过点![]() ,直线
,直线![]() 与y轴交于点B,与图象G交于点C.
与y轴交于点B,与图象G交于点C.
(1)求m的值.
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,C之间的部分与线段BA,BC围成的区域(不含边界)为W.
①当直线l过点![]() 时,直接写出区域W内的整点个数.
时,直接写出区域W内的整点个数.
②若区域W内的整点不少于4个,结合函数图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数,否则称为合数.
其中,1和0既不是质数也不是合数.
材料二:一个较大自然数是质数还是合数通常用“![]() 法”来判断,主要分为三个步骤:
法”来判断,主要分为三个步骤:
第一步,找出大于![]() 且最接近
且最接近![]() 的平方数
的平方数![]() ;
;
第二步,用小于![]() 的所有质数去除
的所有质数去除![]() ;
;
第三步,如果这些质数都不能整除![]() ,那么
,那么![]() 是质数;如果这些质数中至少有一个能整除
是质数;如果这些质数中至少有一个能整除![]() ,那么
,那么![]() 就是合数.
就是合数.
如何判断239是质数还是合数?
第一步,![]() ;
;
第二步,小于16的质数有:2、3、5、7、11、13,用2、3、5、7、11、13依次去除239;
第三步,发现没有质数能整除239,所以239是质数.
材料三:分解质因数就是把一个合数分解成若干个质数的乘积的形式,通过分解质因数可以确定该合数的约数的个数.若![]() …(
…(![]() ,
,![]() ,
,![]() …是不相等的质数,
…是不相等的质数,![]() ,
,![]() ,
,![]() …是正整数),则合数
…是正整数),则合数![]() 共有
共有![]() …个约数.如
…个约数.如![]() ,
,![]() ,则8共有4个约数;又如
,则8共有4个约数;又如![]() ,
,![]() ,则12共有6个约数.请用以上方法解决下列问题:
,则12共有6个约数.请用以上方法解决下列问题:
(1)请用“![]() 法”判断163是质数还是合数;
法”判断163是质数还是合数;
(2)求有12个约数的最小自然数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+b的图象与x轴的交点为A(2,0),与y轴的交点为B,直线AB与反比例函数y=![]() 的图象交于点C(﹣1,m).
的图象交于点C(﹣1,m).
(1)求一次函数和反比例函数的表达式;
(2)直接写出关于x的不等式2x+b>![]() 的解集;
的解集;
(3)点P是这个反比例函数图象上的点,过点P作PM⊥x轴,垂足为点M,连接OP,BM,当S△ABM=2S△OMP时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 也在抛物线
也在抛物线![]() 上(点
上(点![]() 与点
与点![]() 不重合),我们称这样的两条抛物线
不重合),我们称这样的两条抛物线![]() 、
、![]() 互为“友好”抛物线,如图1.
互为“友好”抛物线,如图1.
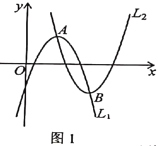
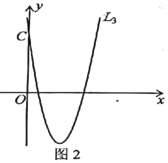
解决问题:如图2,已知物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称,求点
的对称轴对称,求点![]() 的坐标;
的坐标;
(2)求出以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式;
的解析式;
(3)直接写出![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com