【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅，经过测试同时开放2个大餐厅和1个小餐厅，可供3000名学生就餐；同时开放1个大餐厅，1个小餐厅，可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放，那么能否供全校4500名学生就餐？请说明理由.
【答案】（1）1个大餐厅，1个小餐厅分别可供1300名和400名学生就餐；（2）能，见解析.
【解析】
（1）设1个大餐厅可供x名学生就餐、1个小餐厅可供y名学生就餐．根据同时开放2个大餐厅、1个小餐厅，可供3000名学生就餐；同时开放1个大餐厅、1个小餐厅，可供1700名学生就餐列方程组求解即可；
（2）先计算出5个餐厅同时开放容纳的总人数，然后与全校人数比较即可．
解：（1）设1个大餐厅，1个小餐厅分别可供
，
名学生就餐
由题意可知
解得
答：1个大餐厅，1个小餐厅分别可供1300名和400名学生就餐.
（2）∵
∴ 如果3个大餐厅和2个小餐厅全部开放，那么能需足全校的4500名学生的就餐需求.
故答案为（1）1个大餐厅，1个小餐厅分别可供1300名和400名学生就餐；（2）能，见解析.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】有一座抛物线型拱桥，在正常水位时水面
的宽为18米，拱顶
离水面的距离
为9米，建立如图所示的平面直角坐标系.
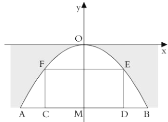
（1）求此抛物线的解析式；
（2）一艘货船在水面上的部分的横断面是矩形
.
①如果限定矩形的长
为12米，那么要使船通过拱桥，矩形的高
不能超过多少米？
②若点
，
都在抛物线上，设
，当
的值最大时，求矩形的高.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，点E是BC边上一动点（不与点C重合）对角线AC与BD相交于点O，连接AE，交BD于点G．
（1）根据给出的△AEC，作出它的外接圆⊙F，并标出圆心F（不写作法和证明，保留作图痕迹）；
（2）在（1）的条件下，连接EF．①求证：∠AEF＝∠DBC；
②记t＝GF2+AGGE，当AB＝6，BD＝6
时，求t的取值范围．
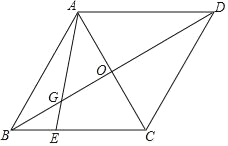
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1的小正方形组成的网格中，四边形ABCD的四个顶点都在格点上，请按要求完成下列各题．
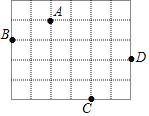
（1）线段AB的长为__，BC的长为__，CD的长为__，AD的长为__；
（2）连接AC，通过计算△ACD的形状是__；△ABC的形状是__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，以AB为直径的⊙O交BC于点D，交AC于点E，连结DE，且BD＝DE，过点B作BP∥DE，交⊙O于点P，连结OP．
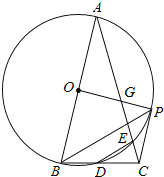
（1）求证：AB＝AC；
（2）若∠A＝30°，求∠BOP的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与
轴交于点A和点B（3，0），与
轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）若点M是抛物线在
轴下方上的动点，过点M作MN//
轴交直线BC于点N，求线段MN的最大值；
（3）在（2）的条件下，当MN取最大值时，在抛物线的对称轴
上是否存在点P，使△PBN是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在
中，
，
，点
、
分别在边
、
上，
，连结
，点
、
、
分别为
、、
的中点．
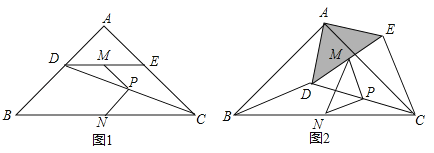
（1）观察猜想图1中，线段
与
的数量关系是_______，位置关系是_______；
（2）探究证明把
绕点
逆时针方向旋转到图2的位置，连结
、
、
，判断
的形状，并说明理由；
（3）拓展延伸把绕点在平面内自由旋转，若
，
，请直接写出面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将含30°角的直角三角板ABC（∠A＝30°）绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得到Rt△A′B′C，A′C与AB交于点D，过点D作DE∥A′B′交CB′于点E，连接BE．易知，在旋转过程中，△BDE为直角三角形．设BC＝1，AD＝x，△BDE的面积为S．
（1）当α＝30°时，求x的值．
（2）求S与x的函数关系式，并写出x的取值范围；
（3）以点E为圆心，BE为半径作⊙E，当S＝
时，判断⊙E与A′C的位置关系，并求相应的tanα值．
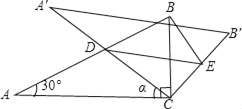
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了迎接2022年的冬奥会，中小学都积极开展冰上运动，小乙和小丁进行500米短道速滑比赛，他们的五次成绩（单位：秒）如表所示：
1 | 2 | 3 | 4 | 5 | |
小乙 | 45 | 63 | 55 | 52 | 60 |
小丁 | 51 | 53 | 58 | 56 | 57 |
设两人的五次成绩的平均数依次为
乙，丁，成绩的方差一次为
，
，则下列判断中正确的是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com