
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).

(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(2,
;(3)(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )或(2,
)或(2,![]() ).
).
【解析】
试题分析:(1)由点B、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设出点M的坐标以及直线BC的解析式,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,结合点M的坐标即可得出点N的坐标,由此即可得出线段MN的长度关于m的函数关系式,再结合点M在x轴下方可找出m的取值范围,利用二次函数的性质即可解决最值问题;
(3)假设存在,设出点P的坐标为(2,n),结合(2)的结论可求出点N的坐标,结合点N、B的坐标利用两点间的距离公式求出线段PN、PB、BN的长度,根据等腰三角形的性质分类讨论即可求出n值,从而得出点P的坐标.
试题解析:(1)将点B(3,0)、C(0,3)代入抛物线![]() 中,得
中,得![]() :,解得:
:,解得:![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ;
;
(2)设点M的坐标为(m,![]() ),设直线BC的解析式为y=kx+3,把点点B(3,0)代入y=kx+3中,得:0=3k+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3.∵MN∥y轴,∴点N的坐标为(m,﹣m+3).∵抛物线的解析式为
),设直线BC的解析式为y=kx+3,把点点B(3,0)代入y=kx+3中,得:0=3k+3,解得:k=﹣1,∴直线BC的解析式为y=﹣x+3.∵MN∥y轴,∴点N的坐标为(m,﹣m+3).∵抛物线的解析式为![]() =
=![]() ,∴抛物线的对称轴为x=2,∴点(1,0)在抛物线的图象上,∴1<m<3.∵线段MN=﹣m+3﹣(
,∴抛物线的对称轴为x=2,∴点(1,0)在抛物线的图象上,∴1<m<3.∵线段MN=﹣m+3﹣(![]() )=
)=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,线段MN取最大值,最大值为
时,线段MN取最大值,最大值为![]() ;
;
(3)假设存在.设点P的坐标为(2,n).
当m=![]() 时,点N的坐标为(
时,点N的坐标为(![]() ,
,![]() ),∴PB=
),∴PB=![]() =
=![]() ,PN=
,PN=![]() ,BN=
,BN=![]() =
=![]() .
.
△PBN为等腰三角形分三种情况:
①当PB=PN时,即![]() =
=![]() ,解得:n=
,解得:n=![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() );
);
②当PB=BN时,即![]() =
=![]() ,解得:n=±
,解得:n=±![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() )或(2,
)或(2,![]() );
);
③当PN=BN时,即![]() =
=![]() ,解得:n=
,解得:n=![]() ,此时点P的坐标为(2,
,此时点P的坐标为(2,![]() )或(2,
)或(2,![]() ).
).
综上可知:在抛物线的对称轴l上存在点P,使△PBN是等腰三角形,点的坐标为(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )、(2,
)、(2,![]() )或(2,
)或(2,![]() ).
).


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点E(﹣4,2),点F(﹣1,﹣1),以点O为位似中心,按比例1:2把△EFO缩小,则点E的对应点E的坐标为( )
A. (2,﹣1)或(﹣2,1) B. (8,﹣4)或(﹣8,4) C. (2,﹣1) D. (8,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)
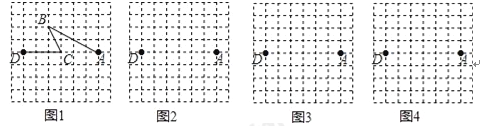
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动±10%,如果以标准价格为标准,超过标准价格记作“+”,低于标准价格记作“-”,那么该商品价格的浮动范围可以怎样表示?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结A0,如果AB=3,AO=2,那么AC的长等于______.
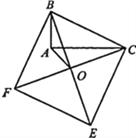
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com