
【题目】有一座抛物线型拱桥,在正常水位时水面![]() 的宽为18米,拱顶
的宽为18米,拱顶![]() 离水面
离水面![]() 的距离
的距离![]() 为9米,建立如图所示的平面直角坐标系.
为9米,建立如图所示的平面直角坐标系.
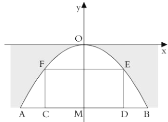
(1)求此抛物线的解析式;
(2)一艘货船在水面上的部分的横断面是矩形![]() .
.
①如果限定矩形的长![]() 为12米,那么要使船通过拱桥,矩形的高
为12米,那么要使船通过拱桥,矩形的高![]() 不能超过多少米?
不能超过多少米?
②若点![]() ,
,![]() 都在抛物线上,设
都在抛物线上,设![]() ,当
,当![]() 的值最大时,求矩形
的值最大时,求矩形![]() 的高.
的高.
【答案】(1)此抛物线的解析式为y=-![]() x2;(2)①要使船通过拱桥,矩形的高DE不能超过5米;②矩形CDEF的高为
x2;(2)①要使船通过拱桥,矩形的高DE不能超过5米;②矩形CDEF的高为![]() 米.
米.
【解析】
(1)根据题意设抛物线的解析式为y=ax2(a≠0).把已知坐标(9,-9)代入解析式求得a即可;
(2)①已知CD=12,把已知坐标代入函数关系式可求解;
②设DM=a米,可得EF=CD=2DM=2a米、DE=FC=9-![]() a2,根据L=EF+DE+CF求得L的值最大时a的值,代入DE=9-
a2,根据L=EF+DE+CF求得L的值最大时a的值,代入DE=9-![]() a2问题可解.
a2问题可解.
解:(1)根据题意,设抛物线解析式为:y=ax2,
将点B(9,-9)代入,得:81a=-9,
解得:a=-![]() ,
,
此抛物线的解析式为y=-![]() x2;
x2;
(2)①当x=6时,y=-![]() ×36=-4,
×36=-4,
∵9-4=5,
∴矩形的高DE不能超过5米,才能使船通过拱桥;要使船通过拱桥,矩形的高DE不能超过5米;
②设DM=a米,则EF=CD=2DM=2a米,
当x=a时,y=-![]() a2,
a2,
∴DE=FC=9-![]() a2,
a2,
则L=2a+2(9-![]() a2)=-
a2)=-![]() a2+2a+18=-
a2+2a+18=-![]() (a-
(a-![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L取得最大值,矩形CDEF的高为
时,L取得最大值,矩形CDEF的高为![]() 米
米


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
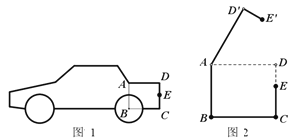
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
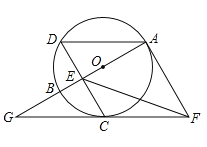
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,若
,若![]() 的半径为4,求
的半径为4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
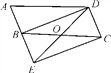
【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,线段
,线段![]() 与
与![]() 轴平行,且
轴平行,且![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和
和![]() ,若线段
,若线段![]() 以每秒2个单位长度的速度向下平移,设平移的时间为
以每秒2个单位长度的速度向下平移,设平移的时间为![]() (秒).若抛物线与线段
(秒).若抛物线与线段![]() 有公共点,则
有公共点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
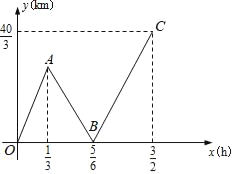
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发.甲,乙两人到达N地后均停止骑行,已知M,N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
(1)求线段BC所在直线的函数表达式;
(2)分别求甲,乙的速度;
(3)填空:点A的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供3000名学生就餐;同时开放1个大餐厅,1个小餐厅,可供1700名学生就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名学生就餐.
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全校4500名学生就餐?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com