
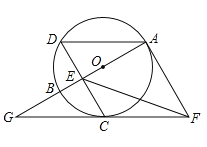
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,若
,若![]() 的半径为4,求
的半径为4,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接![]() ,首先根据垂径定理及
,首先根据垂径定理及![]() 证明
证明![]() 为等边三角形,则有
为等边三角形,则有![]() ,进而可得出
,进而可得出![]() ,再利用平行线的性质和
,再利用平行线的性质和![]() ,证明
,证明![]() ,从而结论可证;
,从而结论可证;
(2)作![]() 于点
于点![]() ,首先证明四边形
,首先证明四边形![]() 为菱形,则有
为菱形,则有![]() ,
,![]() ,再利用平行线的性质进一步得出
,再利用平行线的性质进一步得出![]() ,然后利用特殊角的三角函数值求出EC,CF的长度,从而可求EH,FH,最后利用勾股定理求EF的长度即可.
,然后利用特殊角的三角函数值求出EC,CF的长度,从而可求EH,FH,最后利用勾股定理求EF的长度即可.
(1)证明:如图,连接![]() ,
,
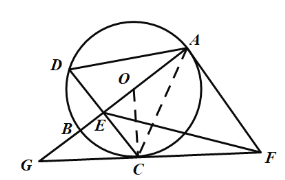
∵![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() .
.
![]() ,
,
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 相切.
相切.
(2)解:如图,作![]() 于点
于点![]() ,
,
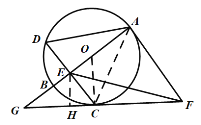
∵![]() 与
与![]() 相切,
相切,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,
,
∴四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ,
,![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解全国中学生最喜爱哪位歌手,适合全面调查.
B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=5,S乙2=0.5,则甲麦种产量比较稳.
C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.
D.一组数据:3,2,5,5,4,6的众数是5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
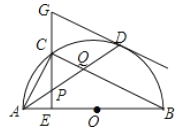
【题目】如图,在![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() ,交于下列结论:
,交于下列结论:
①![]() ;
;
②![]() ;
;
③点![]() 是
是![]() 的外心,
的外心,
④![]()
其中正确结论是_________________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() 是直线
是直线![]() 上的一个动点,直线
上的一个动点,直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .
.
(1)求这个抛物线的解析式;
(2)如图,当点![]() 在线段
在线段![]() 上时,连接
上时,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
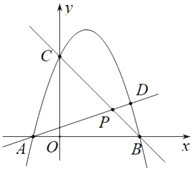
(3)若![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
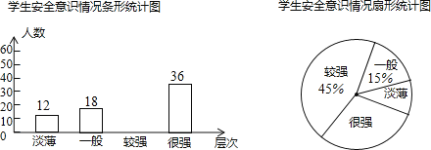
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线型拱桥,在正常水位时水面![]() 的宽为18米,拱顶
的宽为18米,拱顶![]() 离水面
离水面![]() 的距离
的距离![]() 为9米,建立如图所示的平面直角坐标系.
为9米,建立如图所示的平面直角坐标系.
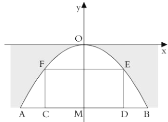
(1)求此抛物线的解析式;
(2)一艘货船在水面上的部分的横断面是矩形![]() .
.
①如果限定矩形的长![]() 为12米,那么要使船通过拱桥,矩形的高
为12米,那么要使船通过拱桥,矩形的高![]() 不能超过多少米?
不能超过多少米?
②若点![]() ,
,![]() 都在抛物线上,设
都在抛物线上,设![]() ,当
,当![]() 的值最大时,求矩形
的值最大时,求矩形![]() 的高.
的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
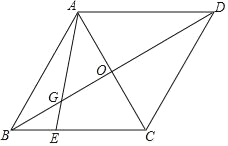
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com