
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() 是直线
是直线![]() 上的一个动点,直线
上的一个动点,直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .
.
(1)求这个抛物线的解析式;
(2)如图,当点![]() 在线段
在线段![]() 上时,连接
上时,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
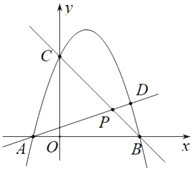
(3)若![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的横坐标为1,2,
的横坐标为1,2,![]() ,
,![]() .
.
【解析】
(1)将![]() ,
,![]() 代入
代入![]() 求
求![]() ;(2)作
;(2)作![]() ,垂足为
,垂足为![]() ,分别过
,分别过![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和平行线
和平行线![]() ,两线交于点
,两线交于点![]() ,得出
,得出![]() ,再根据
,再根据![]() ,设坐标建立等量关系求出
,设坐标建立等量关系求出![]() 点坐标,再求出直线
点坐标,再求出直线![]() 的函数解析式,联立解方程求出
的函数解析式,联立解方程求出![]() 点坐标;(3)分类讨论,利用相似三角形的模型求解.
点坐标;(3)分类讨论,利用相似三角形的模型求解.
(1)将![]() ,
,![]() 代入
代入![]()
得:![]() 解得
解得![]()
∴二次函数的解析式为:![]() ;
;
(2)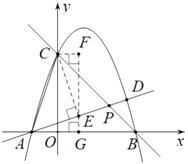
作![]() ,垂足为
,垂足为![]() ,分别过
,分别过![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和平行线
和平行线![]() ,两线交于点
,两线交于点![]() .
.
∵![]() ,∴
,∴![]() .
.
易证![]() ,∴
,∴![]() .设
.设![]() 为
为![]() ,则
,则![]() ,
,![]() ,
,
![]() .
.
∴ ,解得
,解得![]() ,∴点
,∴点![]() .
.
由![]() ,
,![]() 可求得直线
可求得直线![]() 为:
为:![]() ;
;
由![]() ,
,![]() 可求得直线
可求得直线![]() 为:
为:![]() ;
;
二者联立方程组,
解得点![]() 的坐标为
的坐标为![]() ;
;
(3)直线![]() 的解析式为:
的解析式为:![]() 且
且![]() .设
.设![]() 如图:
如图:

①当![]() 在
在![]() 的左侧时:作
的左侧时:作![]() 于
于![]() ,
,![]() 于
于![]()
∴![]() ,
,![]()
∴![]()
∴![]() 代入
代入![]()
解得:![]()
∴ 将![]() 代入则
代入则![]() 的横坐标为1或2;
的横坐标为1或2;
②当![]() 在
在![]() 的右侧时,
的右侧时,![]()
∴![]() 是
是![]() 的中点,设
的中点,设![]() ,
,![]()
∴中点![]() 代入
代入![]()
解得:![]()
将![]() 代入则
代入则![]() 的横坐标为
的横坐标为![]() 或
或![]()
综上所述:点![]() 的横坐标为1,2,
的横坐标为1,2,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知将反比例函数![]() (x<0),沿y轴翻折得到反比例函数
(x<0),沿y轴翻折得到反比例函数![]() (x>0),一次函数y=ax+b与
(x>0),一次函数y=ax+b与![]() 交于A(1,m),B(4,n)两点;
交于A(1,m),B(4,n)两点;
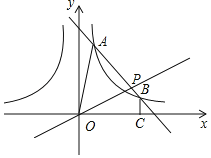
(1)求反比例函数y2和一次函数y=ax+b的解析式;
(2)连接OA,过B作BC⊥x轴,垂足为C,点P是线段AB上一点,若直线OP将四边形OABC的面积分成1:2两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
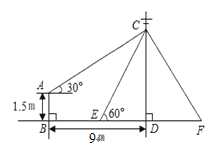
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
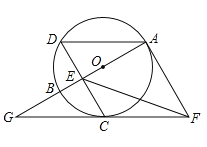
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,若
,若![]() 的半径为4,求
的半径为4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地如图,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数图象;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数图象;请根据图象解答下到问题:
(1)货车离甲地距离y(干米)与时间x(小时)之间的函数式为 ;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
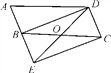
【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
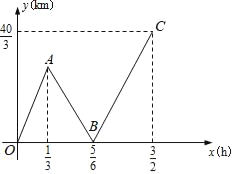
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发.甲,乙两人到达N地后均停止骑行,已知M,N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
(1)求线段BC所在直线的函数表达式;
(2)分别求甲,乙的速度;
(3)填空:点A的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
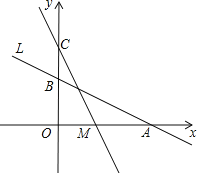
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com