
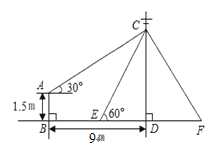
【题目】如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆9m的B处安置高为1.5m的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长.(结果保留根号)
![]()
【答案】拉线CE的长约为(6+![]() )米.
)米.
【解析】
过点A作AH⊥CD,垂足为H,根据矩形性质求出AB,AH,在Rt△ACH中,tan∠CAH=![]() ,可求出CH;在Rt△CDE中,∠CED=60°,sin∠CED=
,可求出CH;在Rt△CDE中,∠CED=60°,sin∠CED=![]() ,可求出CE.
,可求出CE.
解:过点A作AH⊥CD,垂足为H,
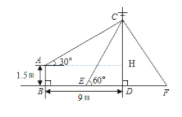
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=9,
在Rt△ACH中,tan∠CAH=![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=9tan30°=9×![]() (米),
(米),
∵DH=1.5,
∴CD=3![]() +1.5,
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED=![]() ,
,
∴CE![]() (米),
(米),
答:拉线CE的长约为(6+![]() )米
)米


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
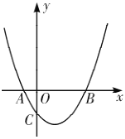
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使
,使![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴1为
,其对称轴1为![]() .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点![]() 在第二象限内的抛物线上,动点
在第二象限内的抛物线上,动点![]() 在对称轴1上.
在对称轴1上.
①当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
②当四边形![]() 的面积最大时,求四边形
的面积最大时,求四边形![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
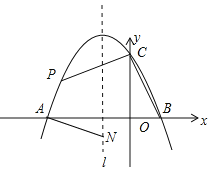
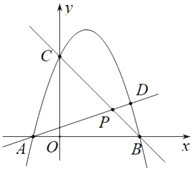
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() 是直线
是直线![]() 上的一个动点,直线
上的一个动点,直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .
.
(1)求这个抛物线的解析式;
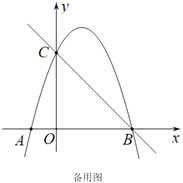
(2)如图,当点![]() 在线段
在线段![]() 上时,连接
上时,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为检测“停课不停学”期间九年级学生的复习情况,进行了中考数学模拟测试并从中随机抽取了部分学生的测试成绩分成![]() 个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
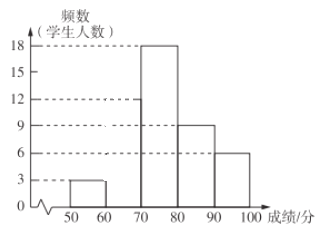
请根据信息回答下列问题:
![]() 若成绩在
若成绩在![]() 分的频率为
分的频率为![]() ,请计算抽取的学生人数并补全频数分布直方图;
,请计算抽取的学生人数并补全频数分布直方图;
![]() 在此次测试中,抽取学生成绩的中位数在______ 分数段中;
在此次测试中,抽取学生成绩的中位数在______ 分数段中;
![]() 若该校九年级共有
若该校九年级共有![]() 名学生,成绩在
名学生,成绩在![]() 分以上的(含
分以上的(含![]() 分)为优秀,请通过计算说明,大约有多少名学生在本次测试中数学成绩为优秀.
分)为优秀,请通过计算说明,大约有多少名学生在本次测试中数学成绩为优秀.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com