
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
【答案】(1)300,250,150;(2)y=﹣50x+800;(3)W=﹣50(x-12)2+800,12元,800元
【解析】试题分析:(1)根据题意得到每涨一元就少50千克,则以13元/千克的价格销售,那么每天售出150千克;(2)根据题意可判断y是x的一次函数.利用待定系数法求解析式,设y=kx+b,把x=10,y=300;x=11,y=250代入即可得到y(千克)与x(元)(x>0)的函数关系式;(2)根据每天获取的利润=每千克的利润×每天的销售量得到W=(x-8)y=(x-8)(-50x+800),然后配成顶点式得y=-50(x-12)2+800,最后根据二次函数的最值问题进行回答即可.
试题解析:(1)∵以11元/千克的价格销售,可售出250千克,
∴每涨一元就少50千克,
∴以13元/千克的价格销售,那么每天售出150千克.
故答案为300,250,150;
(2)y是x的一次函数.设y=kx+b,
∵x=10,y=300;x=11,y=250,
∴![]() ,解得
,解得![]() ,
,
∴y=-50x+800,
经检验:x=13,y=150也适合上述关系式,
∴y=-50x+800.
W=(x-8)y=(x-8)(-50x+800)=-50x2+1200x-6400=-50(x-12)2+800,
∵a=-50<0,
∴当x=12时,W的最大值为800,
即当销售单价为12元时,每天可获得的利润最大,最大利润是800元.


科目:初中数学 来源: 题型:
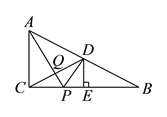
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 是
是![]() 边的中点,过
边的中点,过![]() 作
作![]() 于点
于点![]() ,点
,点![]() 是边
是边![]() 上的一个动点,
上的一个动点, ![]() 与
与![]() 相交于点
相交于点![]() .当
.当![]() 的值最小时,
的值最小时, ![]() 与
与![]() 之间的数量关系是__________.
之间的数量关系是__________.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
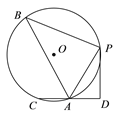
【题目】如图,在⊙O中,B,P,A,C是圆上的点,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
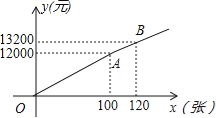
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
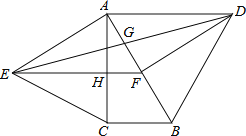
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
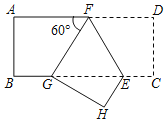
【题目】如图,点E、F分别在矩形ABCD的边BC、AD上,把这个矩形沿EF折叠后,点D恰好落在BC边上的G点处,且∠AFG=60°
(1)求证:GE=2EC;
(2)连接CH、DG,试证明:CH∥DG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为绿化校园,安排七年级三个班植树,其中,一班植树x棵,二班植树的棵数是一班的2倍少20棵,三班植树的棵数是二班的一半多15棵.
(1)三个班共植树多少棵?(用含x的式子表示)
(2)当x=30时,三个班中哪个班植树最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)8÷(﹣2)2﹣4×(﹣3)﹣|﹣6|
(2)(![]() )×(﹣12)
)×(﹣12)
(3)(4x+2y)-3(x-2y)
(4)4ab2-3[a2b-2(a2b-2ab2)]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com