练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算

    （1）8÷（﹣2）2﹣4×（﹣3）﹣|﹣6|

    （2）（ ）×（﹣12）

    （3）（4x+2y）-3(x-2y)

    （4）4ab2-3［a2b-2(a2b-2ab2)］

    【答案】（1）8；（2）－5；（3）x+8y；（4）3a2b-8ab2

    【解析】

    （1）根据有理数的混合运算的法则计算即可；

    （2）利用乘法分配律进行计算；

    （3）先去括号，再合并同类项即可；

    （4）先去括号，再合并同类项即可.

    （1）原式=8÷4+12﹣6

    =2+12﹣6

    =8

    （2）原式=﹣4+9﹣10

    =﹣5

    （3）原式=4x+2y-3x+6y

    =x+8y

    （4）原式=4ab2-3(a2b-2a2b+4ab2)

    =4ab2-3a2b+6a2b-12ab2

    =3a2b-8ab2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．

    小丽：如果以10元/千克的价格销售，那么每天可售出300千克．

    小强：如果每千克的利润为3元，那么每天可售出250千克．

    小红：如果以13元/千克的价格销售，那么每天可获取利润750元．

    【利润=（销售价-进价）销售量】

    （1）请根据他们的对话填写下表：

    销售单价x（元/kg）

    10

    11

    13

    销售量y（kg）




    （2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；

    （3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，观察函数y=|x|的图象，写出它的两条的性质；

    （2）在图1中，画出函数y=|x-3|的图象；

    根据图象判断：函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到；

    （3）①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到；

    ②根据从特殊到一般的研究方法，函数y=|kx+3|（k为常数，k≠0）的图象可以由函数y=|kx|（k为常数，k≠0）的图象经过怎样的平移得到．

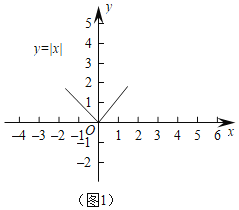
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．

    （1）求证：四边形ABCD是菱形；

    （2）若AB＝，BD＝2，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC中，D是边BC上的一点，且BD：DC=3：5，把△ABC折叠，使点A落在边BC上的点D处，若AM=5，那么AN的长度为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用无刻度的直尺和圆规作出符合要求的图形．(注：不要求写作法，但保留作图痕迹)

    （1）如图，已知线段AB，作一个△ABC，使得∠ACB＝90°；（只需画一个即可）

    （2）如图，已知线段MN，作一个△MPN，使得∠MPN＝90°且sinM＝．（只需画一个即可）

    （1） （2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

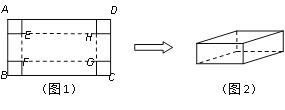
    【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．

    （1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；

    （2）当EH：EF＝7：2，且侧面积与底面积之比为9：7时，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

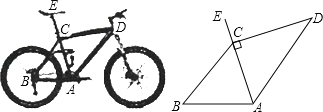
    【题目】为“方便交通，绿色出行”，人们常选择以共享单车作为代步工具、图（1）所示的是一辆自行车的实物图．图（2）是这辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45cm和60cm，且它们互相垂直，座杆CE的长为20cm．点A、C、E在同一条直线上，且∠CAB=75°．

    （参考数据：sin75°=0.966，cos75°=0.259，tan75°=3.732）

    图（1） 图（2）

    （1）求车架档AD的长；

    （2）求车座点E到车架档AB的距离（结果精确到1cm）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

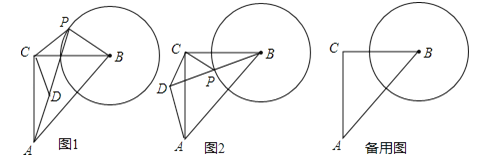
    【题目】如图1．在△ABC中，∠ACB=90°，AC=BC=，以B为圆心、1为半径作圆，设点P为⊙B上一点，线段CP绕着点C顺时针旋转90°，得到线段CD，连接DA、PD、PB．

    （1）求证：AD=BP；

    （2）若DP与⊙B相切，则∠CPB的度数为　　　　　　；

    （3）如图2，当B、P、D三点在同一条直线上时，求BD的长；

    （4）BD的最小值为　　　　　　；BD的最大值为　　　　　　．

    查看答案和解析>>

    同步练习册答案