
【题目】如图,等边△ABC中,D是边BC上的一点,且BD:DC=3:5,把△ABC折叠,使点A落在边BC上的点D处,若AM=5,那么AN的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:由BD:DC=3:5,可设BD=3a,则CD=5a,根据等边三角形的性质和折叠的性质可得:BM+MD+BD=5a,DN+NC+DC=11a,再通过证明△BMD∽△CDN即可求得AM:AN的值,即可求得AN的长.
详解:∵BD:DC=3:5,
∴设BD=3a,则CD=5a,
∵△ABC是等边三角形,
∴AB=BC=AC=8a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=11:13,
∵AM=5,
∴AN=![]() .
.
故选:D.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
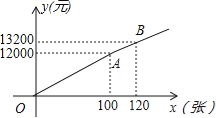
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】福建省教育厅日前发布文件,从2019年开始,体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求,决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价150元,跳绳每条定价30元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一条跳绳;
B网店:足球和跳绳都按定价的90%付款.
已知要购买足球40个,跳绳x条(x>40)
(1)若在A网店购买,需付款 元(用含x的代数式表示).
若在B网店购买,需付款 元(用含x的代数式表示).
(2)若x=100时,通过计算说明此时在哪家网店购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,
并计算需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
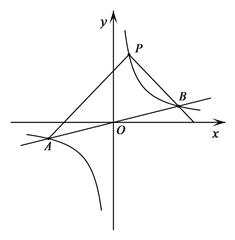
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)8÷(﹣2)2﹣4×(﹣3)﹣|﹣6|
(2)(![]() )×(﹣12)
)×(﹣12)
(3)(4x+2y)-3(x-2y)
(4)4ab2-3[a2b-2(a2b-2ab2)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发生产960件新产品,需要加工后才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独完成这批产品比乙工厂单独完成这批产品多用20天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.5倍,公司需付甲工厂加工费每天80元,乙工厂每天加工费用120元。
(1)求甲、乙两个工厂每天各能加工多少个新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家同时合作完成。在加工过程中,公司派一名工程师每天来厂进行技术指导,并负担每天5元的午餐补助费,请你帮助公司选择一种既省时又省力的方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
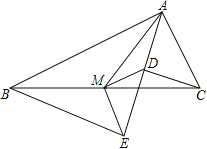
【题目】如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
(1)若AB=8,AC=4,求DE的长;
(2)求证:AB-AC=2DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com