
【题目】某公司开发生产960件新产品,需要加工后才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独完成这批产品比乙工厂单独完成这批产品多用20天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.5倍,公司需付甲工厂加工费每天80元,乙工厂每天加工费用120元。
(1)求甲、乙两个工厂每天各能加工多少个新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家同时合作完成。在加工过程中,公司派一名工程师每天来厂进行技术指导,并负担每天5元的午餐补助费,请你帮助公司选择一种既省时又省力的方案,并说明理由。
【答案】(1)甲工厂每天能加工16件,乙工厂每天能加工24件;(2)选择甲、乙两家工厂合作完成这批产品比较合适,理由见解析.
【解析】
(1)设甲工厂每天能加工x件产品,则乙工厂每天能加工1.5x件产品,根据工作总量除以工作效率等于工作时间,分别表示出甲乙两个工厂单独完成需要的天数,再根据甲比乙多用20天建立方程求解;
(2)分别计算甲乙单独完成需要的天数和费用,以及甲乙合作完成需要的天数和费用,比较三种方案即可得出答案.
(1)设甲工厂每天能加工x件产品,则乙工厂每天能加工1.5x件产品,
依题意得:![]()
解得:![]() .
.
经检验,![]() 是原方程解,也符合题意.
是原方程解,也符合题意.
![]() ,
,
答:甲工厂每天能加工16件,乙工厂每天能加工24件;
(2)甲工厂单独完成需960÷16=60(天),所需费用为80×60+5×60=5100(元)
乙工厂单独完成需960÷24=40(天),所需费用为120×40+5×40=5000(元)
设两个工厂合作完成需![]() (天),所需费用为(80+120)×24+5×24=4920(元).
(天),所需费用为(80+120)×24+5×24=4920(元).
答:通过比较,选择甲、乙两家工厂合作完成这批产品比较合适.


科目:初中数学 来源: 题型:
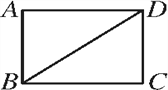
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
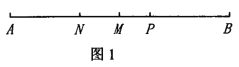
【题目】(1)如图1所示,已知线段AB=20cm,在AB上取一点P,M是AB的中点,N是AP中点,若MN=3cm,求线段AP的长;
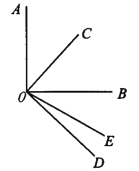
(2)如图2所示,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.则∠COE是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,D是边BC上的一点,且BD:DC=3:5,把△ABC折叠,使点A落在边BC上的点D处,若AM=5,那么AN的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
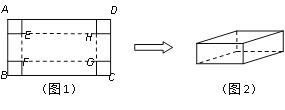
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区教育局为了解今年九年级学生体育测试情况,随机抽查了某班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:


说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下
(1)样本中D级的学生人数占全班学生人数的百分比是 ;
(2)扇形统计图中A级所在的扇形的圆心角度数是 ;
(3)请把条形统计图补充完整;
(4)若该校九年级有500名学生,请你用此样本估计体育测试中A级和B级的学生人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习反比例函数后,为研究新函数![]() ,先将函数变形为
,先将函数变形为![]() ,画图发现函数
,画图发现函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象向上平移1个单位得到.
的图象向上平移1个单位得到.
(1)根据小明的发现,请你写出函数![]() 的图象可以由反比例函数
的图象可以由反比例函数![]() 的图象经过怎样的平移得到;
的图象经过怎样的平移得到;
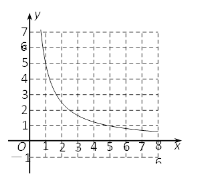
(2)在平面直角坐标系中,已知反比例函数![]() (x>0)的图象如图所示,请在此坐标系中画出函数
(x>0)的图象如图所示,请在此坐标系中画出函数![]() (x>0)的图象;
(x>0)的图象;
(3)若直线y=-x+b与函数![]() (x>0)的图象没有交点,求b的取值范围.
(x>0)的图象没有交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
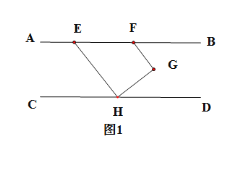
【题目】如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.
(1)求证:∠EHC+∠GFE=180°.
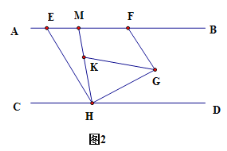
(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.
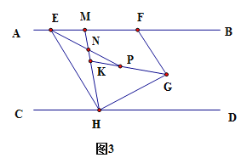
(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com