
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.

科目:初中数学 来源: 题型:
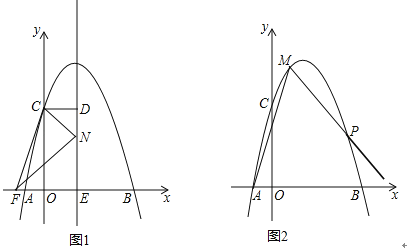
【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣![]() ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
(3)如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
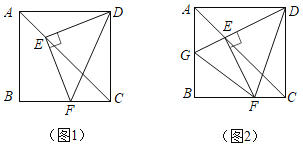
【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
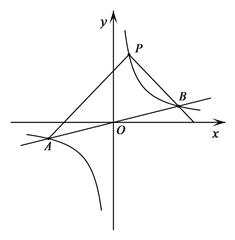
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上表示的数a、b,满足![]()
(1)a的值为______,b的值为______;
(2)已知点M、点N是数轴上的两个动点,点M从点A出发,速度是每秒3个单位,同时点N从点B出发,速度是每秒1个单位:
① 若点M和点N在数轴上相向运动,经过t秒在C处相遇,求t的值和此时点C所表示的数;
② 若点M和点N在数轴上沿着数轴同向运动,经过若干秒,点M和点N相距2个单位,求此时点M和点N表示的数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发生产960件新产品,需要加工后才能投放市场,现甲、乙两个工厂都想加工这批产品,已知甲工厂单独完成这批产品比乙工厂单独完成这批产品多用20天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.5倍,公司需付甲工厂加工费每天80元,乙工厂每天加工费用120元。
(1)求甲、乙两个工厂每天各能加工多少个新产品?
(2)公司制定产品加工方案如下:可以由每个厂家单独完成,也可以由两个厂家同时合作完成。在加工过程中,公司派一名工程师每天来厂进行技术指导,并负担每天5元的午餐补助费,请你帮助公司选择一种既省时又省力的方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
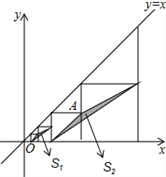
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
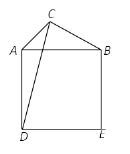
【题目】如图,已知线段 AC=4,线段BC绕点C旋转,且BC=6,连结AB,以AB为边作正方形ADEB,连结CD.
(1)若∠ACB=90°,则AB的值是____;
(2)线段CD长的最大值是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com