
【题目】在平面内,已知∠AOB=50°,OC⊥OA,OD平分∠BOC,则∠AOD的度数为_______.
【答案】60°或30°.
【解析】
分类讨论:OB在∠AOC的内部;OB在∠AOC的外部.根据垂直,可得所成的角是90°,根据角的和差,可得∠BOC的度数,根据角平分线,可得∠BOD的度数,再根据角的和差,可得答案.
符合题意的图形有两个,如图1、图2,
在图1中,OB在∠AOC的内部.
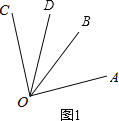
∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=50°,
∴∠BOC=∠AOC-∠AOB=40°.
∵OD平分∠BOC,
∴∠BOD=![]() ∠BOC=20°,∴∠AOD=∠AOB+∠BOD=60°;
∠BOC=20°,∴∠AOD=∠AOB+∠BOD=60°;
在图2中,OB在∠AOC的外部.
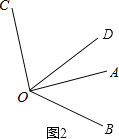
∵OC⊥OA,
∴∠AOC=90°.
∵∠AOB=50°,
∴∠BOC=∠AOB+∠AOC=140°.
∵OD平分∠BOC,
∴∠BOD=![]() ∠BOC=70°,
∠BOC=70°,
∴∠AOD=∠BOD-∠AOB=30°.
综上,∠AOD的度数为60°或30°.
故答案为:60°或30°.


科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点 A 在数轴上对应的数为 a,点B在数轴上对应的数为 b,且 a, b 满足|a+1|+(b-11)![]() =0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
=0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
![]()
(1)求线段 AB 的长;
(2)若 AP=8cm,
①当 C、D 两点运动 1 s 后,求线段 CD 的长;
②当 C、D 两点运动 t s 后,且点 D 在线段 PB 上时,用含t 的代数式表示线段 AC、CD 的长,并说明AC 与 CD 的数量关系.
(3)如果 t=2 s,CD=1 cm,试探索线段 AP 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
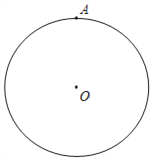
【题目】已知,如图,点A为⊙O上的一点.
(1)用没有刻度的直尺和圆规作一个⊙O的内接正三角形ABC.(保留作图痕迹并标出B、C);
(2)若⊙O半径为10,则三角形ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
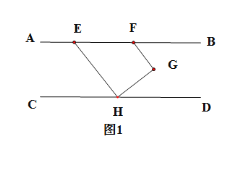
【题目】如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.
(1)求证:∠EHC+∠GFE=180°.
(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.
(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数.
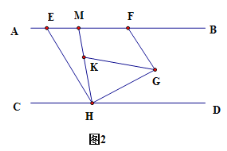
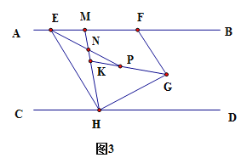
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
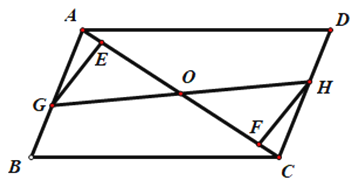
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
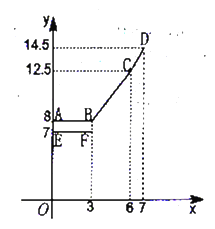
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 的两边分别与射线
的两边分别与射线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.
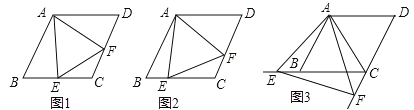
(1)如图1,当点![]() 是线段
是线段![]() 的中点时,请直接写出线段
的中点时,请直接写出线段![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图2,当点![]() 是线段
是线段![]() 上的任意一点(点
上的任意一点(点![]() 不与点
不与点![]() 、
、![]() 重合)时,求证:
重合)时,求证:![]() ;
;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com