
【题目】已知四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 的两边分别与射线
的两边分别与射线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.
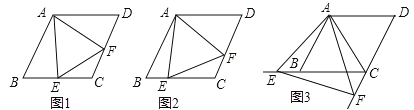
(1)如图1,当点![]() 是线段
是线段![]() 的中点时,请直接写出线段
的中点时,请直接写出线段![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图2,当点![]() 是线段
是线段![]() 上的任意一点(点
上的任意一点(点![]() 不与点
不与点![]() 、
、![]() 重合)时,求证:
重合)时,求证:![]() ;
;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)连接AC,先证△ABC是等边三角形,再由题意得出AE⊥BC,∠B=60°求解可得;
(2)证△BAE≌△CAF即可得;
(3)作AG⊥BC,由∠EAB=15°,∠ABC=60°知∠AEB=45°,根据AG=2![]() 得EG=AG=2
得EG=AG=2![]() ,EB=EG-BG=2
,EB=EG-BG=2![]() -2,再证△AEB≌△AFC知EB=FC,由FD=FC+CD=EB+CD可得答案.
-2,再证△AEB≌△AFC知EB=FC,由FD=FC+CD=EB+CD可得答案.
解:(1)如图1,连接AC,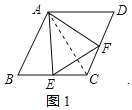
∵四边形ABCD是菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∵E是BC中点,
∴AE⊥BC,BE=![]() BC=
BC=![]() AB
AB
在Rt△ABE中,AE=BEtanB=![]() BE;
BE;
(2)证明:连接![]() ,如图2中,
,如图2中,
∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() 与
与![]() 都是等边三角形,
都是等边三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() .
.
∴![]() .
.

(3)解:连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,如图3所示,
,如图3所示,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
由(2)得![]() ,
,![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
可得![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.



 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
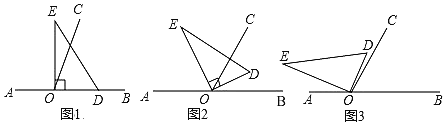
【题目】以直线AB上一点O为端点作射线OC使∠BOC=60°,将一个直角三角形的直角顶点放在O处(注:∠DOE=90°).
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=______;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,则∠BOD=______;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=![]() ∠AOE,求∠BOD的度数.
∠AOE,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1,在△ABC中,AB=AC,CF为AB边上的高,点P为BC边上任意一点,PD⊥AB,PE⊥AC,垂足分别为点D,E.求证:PD+PE=CF.
嘉嘉的证明思路:连结AP,借助△ABP与△ACP的面积和等于△ABC的面积来证明结论.
淇淇的证明思路:过点P作PG⊥CF于G,可证得PD=GF,PE=CG,则PD+PE=CF.
迁移:请参考嘉嘉或淇淇的证明思路,完成下面的问题:
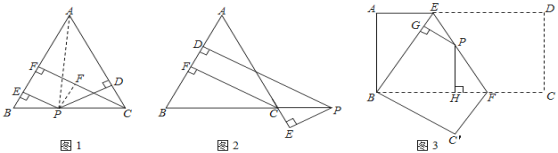
(1)如图2.当点P在BC延长线上时,其余条件不变,上面的结论还成立吗?若不成立,又存在怎样的关系?请说明理由;
(2)当点P在CB延长线上时,其余条件不变,请直接写出线段PD,PE和CF之间的数量关系.
运用:如图3,将矩形ABCD沿EF折叠,使点D落在点B处,点C落在点C′处.若点P为折痕EF上任一点,PG⊥BE于G,PH⊥BC于H,若AD=18,CF=5,直接写出PG+PH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
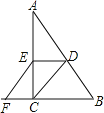
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
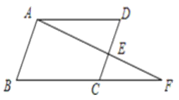
【题目】根据解答过程填空(理由或数学式) :如图,∠DAF=∠F, ∠B=∠D,那么AB与DC平行吗?
解:AB∥DC
∵∠DAF=∠F( ),
∴AD∥BF( )
∴∠D=∠DCF( )
∵∠B=∠D(已知),
∴∠ =∠DCF( )
∴AB∥DC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店出售一种商品,其原价为![]() 元,现有如下两种调价方案:一种是先提价
元,现有如下两种调价方案:一种是先提价![]() ,在此基础上又降价
,在此基础上又降价![]() ;另一种是先降价
;另一种是先降价![]() ,在此基础上又提价
,在此基础上又提价![]() .
.
(1)用这两种方案调价的结果是否一样?调价后的结果是不是都恢复了原价?
(2)两种调价方案改为:一种是先提价![]() ,在此基础上又降价
,在此基础上又降价![]() ;另一种是先降价
;另一种是先降价![]() ,在此基础上又提价
,在此基础上又提价![]() ,这时结果怎样?
,这时结果怎样?
(3)你能总结出什么规律吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
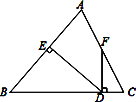
【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=![]() ∠B.
∠B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com