
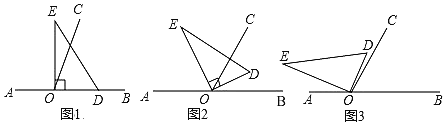
【题目】以直线AB上一点O为端点作射线OC使∠BOC=60°,将一个直角三角形的直角顶点放在O处(注:∠DOE=90°).
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=______;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,则∠BOD=______;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=![]() ∠AOE,求∠BOD的度数.
∠AOE,求∠BOD的度数.
【答案】(1)30°;(2)∠COD=30°;(3)∠BOD的度数为65°.
【解析】
(1)代入∠BOE=∠COE+∠COB求出即可;
(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD=90°,推出∠COD=∠DOB,即可得出答案;
(3)根据平角等于180°求出即可.
(1)∵∠BOE=∠COE+∠COB=90°,
又∵∠COB=60°,
∴∠COE=30°,
故答案为:30°;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=![]() ∠COA,
∠COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB=![]() ∠BOC=30°;
∠BOC=30°;
(3)设∠COD=x,则∠AOE=5x,
∵∠AOE+∠DOE+∠COD+∠BOC=180°,∠DOE=90°,∠BOC=60°,
∴5x+90°+x+60°=180°,
解得x=5°,
即∠COD=5°,
∴∠BOD=∠COD+∠BOC=5°+60°=65°,
∴∠BOD的度数为65°.


科目:初中数学 来源: 题型:
【题目】如图,若点 A 在数轴上对应的数为 a,点B在数轴上对应的数为 b,且 a, b 满足|a+1|+(b-11)![]() =0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
=0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
![]()
(1)求线段 AB 的长;
(2)若 AP=8cm,
①当 C、D 两点运动 1 s 后,求线段 CD 的长;
②当 C、D 两点运动 t s 后,且点 D 在线段 PB 上时,用含t 的代数式表示线段 AC、CD 的长,并说明AC 与 CD 的数量关系.
(3)如果 t=2 s,CD=1 cm,试探索线段 AP 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
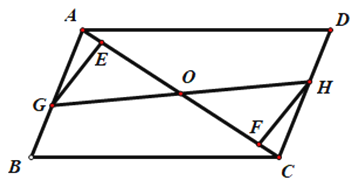
【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
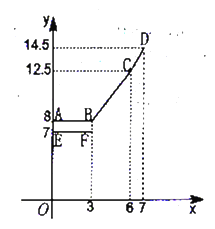
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
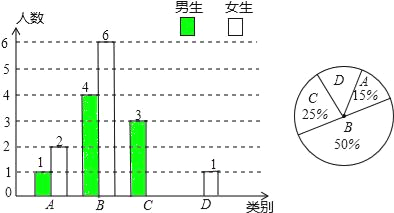
【题目】自实施新教育改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分同学进行了为期半个月的跟踪调查,并将调查结果分为四类:A.特别好;B.好;C.一般;D.较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了多少名同学?
(2)求出调查中C类女生及D类男生的人数,将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的面积等于25,直线a,b,c分别过A,B,C三点,且a∥b∥c,EF⊥直线c,垂足为点F交直线a于点E,若直线a,b之间的距离为3,则EF=( )
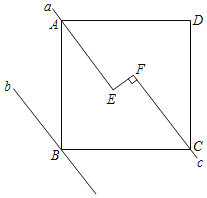
A. 1B. 2C. ![]() -3D. 5-
-3D. 5-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 的两边分别与射线
的两边分别与射线![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() ,且
,且![]() .
.
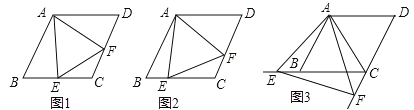
(1)如图1,当点![]() 是线段
是线段![]() 的中点时,请直接写出线段
的中点时,请直接写出线段![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)如图2,当点![]() 是线段
是线段![]() 上的任意一点(点
上的任意一点(点![]() 不与点
不与点![]() 、
、![]() 重合)时,求证:
重合)时,求证:![]() ;
;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com