
【题目】已知,如图,点A为⊙O上的一点.
(1)用没有刻度的直尺和圆规作一个⊙O的内接正三角形ABC.(保留作图痕迹并标出B、C);
(2)若⊙O半径为10,则三角形ABC的面积为 .
【答案】(1)答案见解析;(2)![]() .
.
【解析】分析: (1)以OA为半径,在圆上依次截取得到圆的6等份点,从而得到圆的三等份点,于是可作出⊙O的内接正三角形ABC;
(2)连接OB、OC,延长AO交BC于点D,则AD⊥BC,先求得OD=BOcos60°=5,BD=BOsin60°=5![]() ,据此知BC=2BD=10
,据此知BC=2BD=10![]() 、AD=AO+OD=15,根据三角形的面积公式可得答案.
、AD=AO+OD=15,根据三角形的面积公式可得答案.
详解: (1)如图所示,△ABC即为所求:
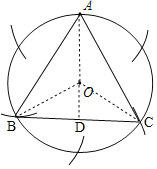
(2)如图,连接OB、OC,延长AO交BC于点D,则AD⊥BC,
∵∠BOC=2∠BAC=120°,
∴∠BOD=60°,
则OD=BOcos60°=10×![]() =5,BD=BOsin60°=10×
=5,BD=BOsin60°=10×![]() =5
=5![]() ,
,
∴BC=2BD=10![]() 、AD=AO+OD=15,
、AD=AO+OD=15,
∴S△ABC=![]() BCAD=
BCAD=![]() ×10
×10![]() ×15=75
×15=75![]() ,
,
故答案为:75![]() .
.
点睛: 本题考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】点A、B在数轴上表示的数a、b,满足![]()
(1)a的值为______,b的值为______;
(2)已知点M、点N是数轴上的两个动点,点M从点A出发,速度是每秒3个单位,同时点N从点B出发,速度是每秒1个单位:
① 若点M和点N在数轴上相向运动,经过t秒在C处相遇,求t的值和此时点C所表示的数;
② 若点M和点N在数轴上沿着数轴同向运动,经过若干秒,点M和点N相距2个单位,求此时点M和点N表示的数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段![]() 上有一点
上有一点![]() ,当
,当![]() 时,则称点
时,则称点![]() 为线段
为线段![]() 的中点.已知数轴上
的中点.已知数轴上![]() ,
,![]() 两点对应数分别为
两点对应数分别为![]() 和
和![]() ,
,![]() ,
,![]() 为数轴上一动点,对应数为
为数轴上一动点,对应数为![]() .
.
(1)若点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点对应的数
点对应的数![]() 为______.若
为______.若![]() 为线段
为线段![]() 的中点时则
的中点时则![]() 点对应的数
点对应的数![]() 为______.
为______.
(2)若点![]() 、点
、点![]() 同时向左运动,它们的速度都为1个单位长度/秒,与此同时点
同时向左运动,它们的速度都为1个单位长度/秒,与此同时点![]() 从-16处以2个单位长度/秒向右运动.
从-16处以2个单位长度/秒向右运动.
①设运动的时间为![]() 秒,直接用含
秒,直接用含![]() 的式子填空
的式子填空
![]() ______;
______;![]() ______.
______.
②经过多长时间后,点![]() 、点
、点![]() 、点
、点![]() 三点中其中一点是另外两点的中点?
三点中其中一点是另外两点的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
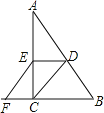
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com