
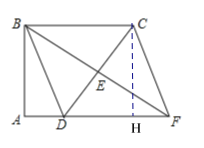
【题目】如图,在四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,点E是边CD的中点,连接BE并延长交AD的延长线于点F,连接CF.
(1)求证:四边形BDFC是平行四边形;
(2)若CB=CD,求四边形BDFC的面积.

【答案】(1)见解析 (2)3![]()
【解析】
(1)证明△BEC△FED,利用一组对边平行且相等的四边形是平行四边形即可判定.
(2)过C点作CH⊥AF,可证四边形ABCH为矩形,求得DH的长,利用勾股定理求出CH的长,利用平行四边形的面积公式即可求解.
(1)∵∠A=∠ABC=90°
∴BC∥AF
∴∠BCD=∠FDE,∠CBE=∠DFE
又∵点E是边CD的中点
∴CE=DE
∴△BCE△FDE(AAS)
∴BC=DF
又BC∥DF
∴四边形BDFC是平行四边形
(2) )过C点作CH⊥AF于H点.
则∠AHC=∠A=∠ABC=90°
∴四边形ABCH为矩形
∴AH=BC=3
∵AD=1
∴DH=2
又∵CB=CD
∴CD=3
根据勾股定理得:CH=![]()
∴S四边形BDFC=3![]()


科目:初中数学 来源: 题型:
【题目】李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师从咸宁出发到外地参加教育信息化应用技术提高培训,他可以乘坐普通列车,也可以乘坐高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍.若高铁的平均速度(千米/小时)是普通列车平均速度的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
已知:如图1,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的
,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的![]() 、
、![]() 与
与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中![]() 、
、![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
②补全图4,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
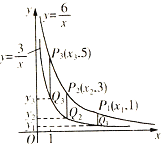
【题目】两个反比例函数![]() ,
,![]() 在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数![]() 图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;
图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;
共2005个连续奇数,过点P1,P2,P3,……,P2005分别作![]() 轴的平行线,与
轴的平行线,与![]() 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则![]() _____________.
_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在四边形ABFC中,![]() =90
=90![]() 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE

(1)试探究,四边形BECF是什么特殊的四边形;
(2)当![]() 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
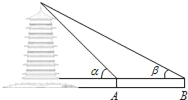
【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)( )
≈1.732)( )
A. 36.21米 B. 37.71米 C. 40.98米 D. 42.48米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,![]() 轴于点C,交的图象于点
轴于点C,交的图象于点![]() 轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )

A. ![]() 与
与![]() 的面积相等
的面积相等
B. 当点A是PC的中点时,点B一定是PD的中点
C. 只有当四边形OCPD为正方形时,四边形PAOB的面积最大
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由如图给出了若干个边长为![]() 和边长为
和边长为![]() 的小正方形纸片及若干个边长为
的小正方形纸片及若干个边长为![]() 的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到
的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到![]()
![]()
请解答下列问题:
(1)请写出如图中所表示的数学等式:______________________________;
(2)用(1)中所得到的结论,解决下面的问题:已知![]() 则
则![]() 的值为_________.
的值为_________.
(3)①请按要求利用所给的纸片拼出一个长方形,要求所拼出图形的面积为![]() 并将所拼出的图像画在的方框中;
并将所拼出的图像画在的方框中;
②再利用另一种计算面积的方法,可将多项式![]() 分解因式,即
分解因式,即![]() _________.
_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com