
【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理绘制成下面的统计图(图1,图2).

小明发现每月每户的用水量在5m3-35m3之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变,根据小明绘制的图表和发现的信息,完成下列问题:
(Ⅰ)n= ,小明调查了 户居民,并补全图2;
(Ⅱ)每月每户用水量的中位数和众数分别落在什么范围?
(Ⅲ)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?
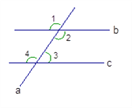
解:∵ ∠1=∠2 (_________________________)
∠1+∠2=230°
∴∠1 =∠2 =________(填度数)
∵ b∥c
∴∠4 =∠2= ________(填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =_________(填度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2a2+3ab-2a-1,B=-a2+ab+1.
(1)若 |a+1| b- 22 0 ,求4A-(3A-2B)的值;
(2)若(1)中代数式的值与a的取值无关,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
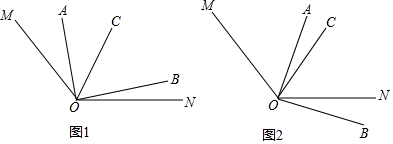
(1)在图1中,若∠AOC=40°,则∠BOC= °,∠NOB= °.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系( 必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电话计费问题,下表中有两种移动电话计费方式:

温馨揭示:方式一:月使用费固定收(月收费:38元/月);主叫不超限定时间不再收费(80分钟以内,包括80分钟);主叫超时部分加收超时费(超过部分0.15元/![]() );被叫免费。
);被叫免费。
方式二:月使用费0元(无月租费);主叫限定时间0分钟;主叫每分钟0.35元/![]() ;被叫免费。
;被叫免费。
(1)设一个月内用移动电话主叫时间为![]() ,方式一计费
,方式一计费![]() 元,方式二计费
元,方式二计费![]() 元。写出
元。写出![]() 和
和![]() 关于
关于![]() 的函数关系式。
的函数关系式。
(2)在平面直角坐标系中画出(1)中的两个函数图象,记两函数图象交点为点![]() ,则点
,则点![]() 的坐标为_____________________(直接写出坐标,并在图中标出点
的坐标为_____________________(直接写出坐标,并在图中标出点![]() )。
)。
(3)根据(2)中函数图象,请直接写出如何根据每月主叫时间选择省钱的计费方式。
查看答案和解析>>
科目:初中数学 来源: 题型:
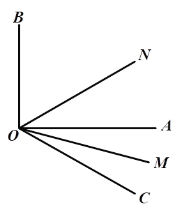
【题目】如图∠AOB是直角,在∠AOB外作射线OC,OM平分∠AOC,ON平分∠BOC.
(1)若∠AOC=38°,求∠MON的度数;
(2)若∠AOC=![]() ,试说明∠MON的大小与
,试说明∠MON的大小与![]() 无关.
无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
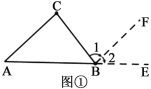
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
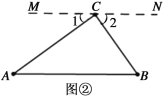
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
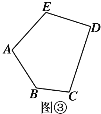
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com