
����Ŀ����ͼ1����֪��MON=140�㣬��AOC���BOC���࣬OCƽ�֡�MOB��
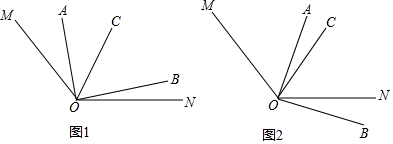
��1����ͼ1�У�����AOC=40�������BOC= �㣬��NOB= �㣮
��2����ͼ1�У����AOC=������NOB=������̽��������֮���������ϵ�� ����д����������Ҫ���̣���ÿһ�����治��д�����ɣ���
��3������֪���������ǰ���£�����AOB���ŵ�O˳ʱ��ת������ͼ2��λ�ã���ʱ������֮���������ϵ�Ƿ���������������˵�����ɣ�������������ֱ��д����ʱ������֮���������ϵ��
���𰸡��⣺��1��50��40����2����=2����40��;��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40��.
��������
��1���ȸ�����ǵĶ�������BOC=50�������ɽ�ƽ���ߵĶ�������BOM=100�������ݽǵIJ�ɵá�BON�Ķ�����
��2��ͬ���ȼ����MOB=2��BOC=2��90��-����=180��-2�����ٸ��ݡ�BON=��MON-��BOM�е�ʽ���ɣ�
��3��ͬ���ɵá�MOB=180��-2�����ٸ��ݡ�BON+��MON=��BOM�е�ʽ���ɣ�
��1����ͼ1��
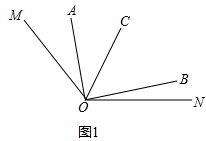
�ߡ�AOC���BOC���࣬
���AOC+��BOC=90����
�ߡ�AOC=40����
���BOC=50����
��OCƽ�֡�MOB��
���MOC=��BOC=50����
���BOM=100����
�ߡ�MON=40����
���BON=��MON-��BOM=140��-100��=40����
��2����=2��-40���������ǣ�
��ͼ1���ߡ�AOC=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�֡ߡ�MON=��BOM+��BON��
��140��=180��-2��+��������=2��-40�㣻
��3������������ʱ��ʱ������֮���������ϵΪ��2��+��=40�㣬
�����ǣ���ͼ2��
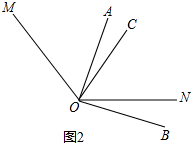
�ߡ�AOC=������NOB=����
���BOC=90��-����
��OCƽ�֡�MOB��
���MOB=2��BOC=2��90��-����=180��-2����
�ߡ�BOM=��MON+��BON��
��180��-2��=140��+������2��+��=40�㣬
�𣺲���������ʱ��ʱ������֮���������ϵΪ��2��+��=40.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣺
�ٺ���![]() ��ż�������������溯����
��ż�������������溯����
����֪�ع�ֱ�߷���Ϊ![]() �������������Ϊ
�������������Ϊ![]() ����
����![]() ��
��
�ۺ���![]() ͼ����ڵ�
ͼ����ڵ�![]() �Գ�����
�Գ�����![]() �ϵ���������
�ϵ���������
�ܸ��ݵ����������������ƶ��Ҫ������ijũҵ���ò��ž����ɳ���λ���ר�Ҷ�����ƶ���������е��У�ÿ������������Dzһλר�ң����мס�����λר����Ҫ��Dz��ͬһ��������ͬ����Dz����������![]() �֣�
�֣�
����֪˫����![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ����
����![]() ��ֱ�߽�˫������֧��
��ֱ�߽�˫������֧��![]() ���㣬��
���㣬��![]() ����
����![]() ����˫���ߵ�������Ϊ
����˫���ߵ�������Ϊ![]() .
.
������ȷ���������Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݸ��������ἰ��֪�����������������⣺
![]()
��1����֪��A��B��C��ʾ�����ֱ�Ϊ1����2.5����3�۲����ᣬB��C����֮��ľ���Ϊ�� �������A�ľ���Ϊ3�ĵ��ʾ�������� ����
��2�����������۵���ʹ��A����C���غϣ�����B���غϵĵ��ʾ�������� ��������������M��N����֮��ľ���Ϊ2020��M��N����ࣩ���ҵ�A����C���غ�ʱ��M����N��Ҳǡ���غϣ���MM�����ʾ�����ֱ��ǣ�M���� ����N���� ����
��3����������P��Q�����ľ���Ϊm��P��Q��ࣩ����ʾ��n�ĵ㵽P��Q����ľ�����ȣ��������۵���ʹ��P����Q���غ�ʱ��P��Q�����ʾ�����ֱ�Ϊ��P�� ����Q�� �������ú�m��n��ʽ�ӱ�ʾ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
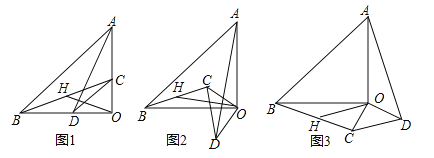
����Ŀ����2017������ʡ������������֪����AOB�͡�COD��Ϊ����ֱ�������Σ���AOB=��COD=90�㣮����AD��BC����HΪBC�е㣬����OH��
��1����ͼ1��ʾ����֤��OH=![]() AD��OH��AD������֤����
AD��OH��AD������֤����
��2������COD�Ƶ�O��ת��ͼ2��ͼ3��ʾλ��ʱ���߶�OH��AD���������Ĺ�ϵ����ѡ��һ��ͼ��֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˼���ס���������������ͬһ�������ֱ���ĺϸ�������������ȡ��10����Ʒ���м�⣬��֪�����ֱ����Ϊ�����������������£�����λ��![]() ��
��
170��174 | 175��179 | 180��184 | 185��189 | |
�׳��� | 1 | 3 | 4 | 2 |
�ҳ��� | 0 | 6 | 2 | 2 |
��1���ֱ����ס������������������ֱ����ƽ������
��2��ֱ��˵���ס������������������ֱ������λ�������ĸ�С���ڣ������Ƿ�������Ӧ��С���ڣ�
��3�����������ֱ����![]() �ķ�Χ��Ϊ�ϸס�����������һ���������������ֱ���ϸ��ʸߣ�
�ķ�Χ��Ϊ�ϸס�����������һ���������������ֱ���ϸ��ʸߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�����ú����ڼ��߷�ο��ƶ����ͥѧ��������ÿλƶ����ͥѧ������һ��ѧϰ��Ʒ��ѧϰ��Ʒÿ���ۼ�60Ԫ��ij�̳������������Ź���50�����ϣ��Żݷ���������һ��5��ѧϰ��Ʒ���ܰ���������ͣ�ʣ�µ�ѧϰ��Ʒ���ۼ۴���ۣ����������������ѧϰ��Ʒȫ�����ۼ۴������.
��1����У�ɹ���ʦ���֣���У����ѡ�������Ź�������Ҫ����Ǯ��һ���ģ��ʸ�У��Ҫ������ٷ�ѧϰ��Ʒ��
��2������У�ı�ƻ����蹺��ѧϰ��Ʒ80�ݣ�ѡ�����ַ����Żݣ�˵�����ɣ������ѡ��÷����Żݵİٷ�������ȷ��1%��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB��CD��ACƽ�֡�BAD��CE��AD��AB��E��
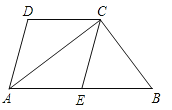
��1����֤���ı���AECD�����Σ�
��2������E��AB���е㣬���ж���ABC����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=ax2��![]() ax��4a��x�ύ��A��B���㣬��y�ύ��C�㣬A����B����࣬C����x���·����ҡ�AOC�ס�COB
ax��4a��x�ύ��A��B���㣬��y�ύ��C�㣬A����B����࣬C����x���·����ҡ�AOC�ס�COB
��1�������������ߵĽ���ʽ��ֱ��BC�Ľ���ʽ��
��2�����DΪ�����߶Գ����ϵ�һ�㣬����D�ڶԳ������˶�ʱ���Ƿ�������C��A��B���㣬�������ε��ĸ����㣿�����ԣ������D���꣬�������ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
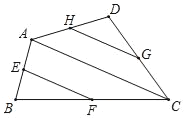
����Ŀ����ͼ����E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��DA���е㣮
��1�����ͼ���߶ζ��ɻ��������߶Σ���ô����Щ�����߶�����ʾ�������У�������![]() ��ȵ��������� ����
��ȵ��������� ����
��2����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����������
����������![]() ��
��![]() ��
��![]() ��ʾ����������
��ʾ����������![]() ���� ����
���� ����![]() ���� ����
���� ����
��3��������![]()
![]() ��������ԭͼ����ͼ����Ҫ��д��������Ҫд�����ۣ�
��������ԭͼ����ͼ����Ҫ��д��������Ҫд�����ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com