
����Ŀ�������������⣺
�ٺ���![]() ��ż�������������溯����
��ż�������������溯����
����֪�ع�ֱ�߷���Ϊ![]() �������������Ϊ
�������������Ϊ![]() ����
����![]() ��
��
�ۺ���![]() ͼ����ڵ�
ͼ����ڵ�![]() �Գ�����
�Գ�����![]() �ϵ���������
�ϵ���������
�ܸ��ݵ����������������ƶ��Ҫ������ijũҵ���ò��ž����ɳ���λ���ר�Ҷ�����ƶ���������е��У�ÿ������������Dzһλר�ң����мס�����λר����Ҫ��Dz��ͬһ��������ͬ����Dz����������![]() �֣�
�֣�
����֪˫����![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ����
����![]() ��ֱ�߽�˫������֧��
��ֱ�߽�˫������֧��![]() ���㣬��
���㣬��![]() ����
����![]() ����˫���ߵ�������Ϊ
����˫���ߵ�������Ϊ![]() .
.
������ȷ���������Ϊ_____.
���𰸡��ڢۢ�
��������
������������Ķ�������������Ľ���ʽ��������ż�ԵĶ��弴���жϢ٣����ݻع�ֱ�߹��������ĵ㣬���뼴���жϢڣ��������Һ��������ʣ�������֤��������뼴���жϢۣ����÷������ԭ���Լ�����������жϢܣ�����˫���ߵĶ����Լ������ʹ�ʽ�����жϢ�.
�ٺ����Ķ�����Ϊ![]() ��
��![]() �������溯������ż�������ʴ���
�������溯������ż�������ʴ���
�ڸ��ݻع�ֱ�߷��̺�����������ĵ㣬��![]() ����ع鷽�̿ɵ�
����ع鷽�̿ɵ�![]() ������ȷ��
������ȷ��
�۰�![]() ���뺯��
���뺯��![]() ������ֵΪ
������ֵΪ![]() �����Ժ���
�����Ժ���![]() ����
����![]() �Գƣ���
�Գƣ���![]() ���ɵú���
���ɵú���![]() �ĵ�����������Ϊ
�ĵ�����������Ϊ![]() �����Ժ���
�����Ժ���![]() ��
��![]() ���ǵ�����.����ȷ��
���ǵ�����.����ȷ��
�ܸ������⣬��![]() ��������ۣ���һ�֣�
��������ۣ���һ�֣�![]() �˷ֳ�
�˷ֳ�![]() �����飬
�����飬
������![]() �˷ֵ�ͬһ����������
�˷ֵ�ͬһ����������![]() ����������ѡ
����������ѡ![]() �������ż��ң���
�������ż��ң���![]() �������
�������
��ʣ�µ�![]() �˷ֳ�
�˷ֳ�![]() �飬��
�飬��![]() �ַ��鷽������
�ַ��鷽������![]() ��ȫ���У����ŵ�����
��ȫ���У����ŵ�����![]() ��������
��������
��![]() ����������ʱ��
����������ʱ��![]() �ְ��ŷ�����
�ְ��ŷ�����
�ڶ��֣�![]() �˷ֳ�
�˷ֳ�![]() �����飬���������������е�
�����飬���������������е�![]() �ˣ�һ���ŵ�ͬһ������
�ˣ�һ���ŵ�ͬһ������
������![]() ������ѡ
������ѡ![]() �ˣ������һ���ŵ�һ����������
�ˣ������һ���ŵ�һ����������![]()
![]() �������
�������
��ʣ�µ�![]() ��ȫ���У����ŵ�����
��ȫ���У����ŵ�����![]() ����������
����������![]() �������
�������
���ʱ��![]() �ְ��ŷ�������һ����
�ְ��ŷ�������һ����![]() �ְ��ŷ���.�ʴ���.
�ְ��ŷ���.�ʴ���.
����![]() Ϊ˫������֧��һ�㣬��
Ϊ˫������֧��һ�㣬��![]() ��
��![]() ��
��

��ֱ��������![]() �У�
��![]() ��
��
��˫���ߵĶ����֪��![]() ��
��
��![]() ������
������![]() ��
��
��Ϊ![]() ��
��
![]()
![]() �����
�����![]() .
.
![]()
![]() ��
��
�ɹ��ɶ����ɵã�![]() ����
����![]() .����ȷ.
.����ȷ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
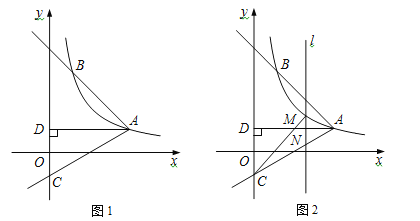
����Ŀ����ͼ1������������![]() ��x��0����ͼ����A��
��x��0����ͼ����A��![]() ��1��������AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC��75�㣬AD��y��������ΪD��
��1��������AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC��75�㣬AD��y��������ΪD��
��1����k��ֵ��
��2����tan��DAC��ֵ��ֱ��AC�Ľ���ʽ��
��3����ͼ2��M���߶�AC�Ϸ�����������ͼ����һ��������M��ֱ��l��x������AC�ཻ�ڵ�N������CM�����CMN��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
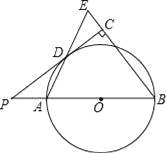
����Ŀ������ͼ����֪AB�ǡ�O��ֱ������P��BA���ӳ����ϣ�PD�С�O�ڵ�D������B��BE��ֱ��PD����PD���ӳ����ڵ�C������AD���ӳ�����BE�ڵ�E��
��1����֤��AB=BE��
��2����PA=2��cosB=![]()
![]() �����O�뾶�ij���
�����O�뾶�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
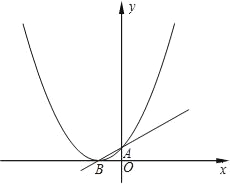
����Ŀ����֪������y=ax2+x+1��ͼ����x��ֻ��һ�������㣮
��1�������������ϵʽ��
��2����ͼ��ʾ������κ���y=ax2+x+1ͼ��Ķ���ΪB����y��Ľ���ΪA��PΪͼ���ϵ�һ�㣬�����߶�PBΪֱ����Բ��ֱ��AB�����ڵ�B����P������ꣻ
��3���ڣ�2���У���Բ��x����һ�������ֱ��PB�ĶԳƵ�ΪM����̽����M�Ƿ���������y=ax2+x+1�ϣ������������ϣ����M������ꣻ�����ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014��1�£����ҷ���ί��ָ̨�������Ҫ��2015���ǰ�����г���ԭ����ȫ��ʵ�о������ˮ���ƶȣ�С��Ϊ�˽�����������ˮ�۷�������ᷴ�죬����������Լ���סС���IJ��־�����ÿ��ÿ������ˮ�����������۶���ˮ��Ϊ�ı�������������е��飬���ѵ������������Ƴ������ͳ��ͼ��ͼ1��ͼ2����

С������ÿ��ÿ������ˮ����5m3-35m3֮�䣬��8���������ˮ�۸�����Ƿ�������ν�����ῼ����ˮ��ʽ�ĸı䣬����С�����Ƶ�ͼ���ͷ��ֵ���Ϣ������������⣺
����n= ��С�������� ��������ȫͼ2��
����ÿ��ÿ����ˮ������λ���������ֱ�����ʲô��Χ��
�������С������С����1800����������������ӵ����Ƿ���ȡ��Ӧ����ˮ��ʽ�ı����ľ������ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����֪����![]() ���������ϱ�ʾ5�ĵ���ԭ��(����ʾ0�ĵ�)֮��ľ���.����ʽ��
���������ϱ�ʾ5�ĵ���ԭ��(����ʾ0�ĵ�)֮��ľ���.����ʽ��![]() ,���������ϵ������DZ�ʾ6�ĵ����ʾ3�ĵ�֮��ľ���.����A��B�������Ϸֱ��ʾ��a��b,��A��B����ľ���ɱ�ʾΪ:|AB|=
,���������ϵ������DZ�ʾ6�ĵ����ʾ3�ĵ�֮��ľ���.����A��B�������Ϸֱ��ʾ��a��b,��A��B����ľ���ɱ�ʾΪ:|AB|=![]() .����
.����
������Ϣ���ش��������⣺
(1)�����ϱ�ʾ2��5������֮��ľ����� �������ϱ�ʾ-2��-5������֮��ľ����� .
��2����A��B�������Ϸֱ��ʾʵ��x��![]() .
.
���ô���ʽ��ʾA��B����֮��ľࣻ
�����![]() ,��x��ֵ.
,��x��ֵ.
��3��ֱ��д������ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����ݣ�x1��x2��x3��x4��x5��x6��ƽ������2��������3������һ�����ݣ�3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��3x6��2��ƽ�����ͷ���ֱ��ǣ�������
A. 2��3 B. 2��9 C. 4��25 D. 4��27
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪��MON=140�㣬��AOC���BOC���࣬OCƽ�֡�MOB��
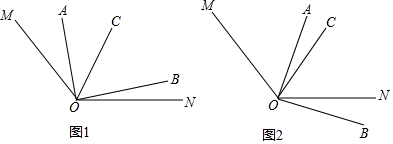
��1����ͼ1�У�����AOC=40�������BOC= �㣬��NOB= �㣮
��2����ͼ1�У����AOC=������NOB=������̽��������֮���������ϵ�� ����д����������Ҫ���̣���ÿһ�����治��д�����ɣ���
��3������֪���������ǰ���£�����AOB���ŵ�O˳ʱ��ת������ͼ2��λ�ã���ʱ������֮���������ϵ�Ƿ���������������˵�����ɣ�������������ֱ��д����ʱ������֮���������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com