
【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=![]()
![]() ,求⊙O半径的长.
,求⊙O半径的长.
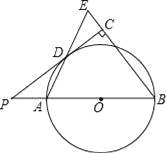
【答案】(1)证明见解析;(2)3.
【解析】试题分析:(1)连接OD,由PD切⊙O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结果;
(2)由(1)知,OD∥BE,得到∠POD=∠B,根据三角函数的定义即可得到结果.
试题解析:(1)证明:连接OD,
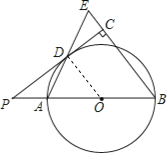
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴∠ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:由(1)知,OD∥BE,
∴∠POD=∠B,
∴cos∠POD=cosB=![]() ,
,
在Rt△POD中,cos∠POD=![]() ,
,
∵OD=OA,PO=PA+OA=2+OA,
∴![]() ,
,
∴OA=3,
∴⊙O半径=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
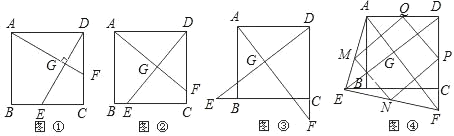
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.

小明发现每月每户的用水量在5m2-35m2之间,有8户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)n= ,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在的小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
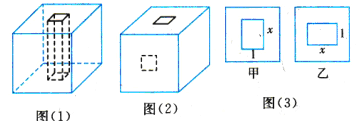
【题目】用橡皮泥做一个棱长为4cm的正方体.
(1)如图(1),在顶面中心位置处从上到下打一个边长为1cm的正方形通孔,打孔后的橡皮泥的表面积是多少?;
(2)如果在第(1)题打孔后,再在正面中心位置处(按图(2)中的虚线)从前到后打一个边长为1cm的正方形通孔,那么打孔后的橡皮泥的表面积为是多少?;
(3)如果把第(2)题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔,能不能使所得橡皮泥的表面积为130cm2?如果能,请求出x;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4![]() ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
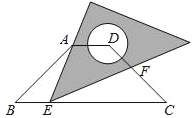
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出以下命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
③函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
④根据党中央关于“精准”脱贫的要求,我州某农业经济部门决定派出五位相关专家对三个贫困地区进行调研,每个地区至少派遣一位专家,其中甲、乙两位专家需要派遣至同一地区,则不同的派遣方案种数有![]() 种;
种;
⑤已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交双曲线右支于
的直线交双曲线右支于![]() 两点,且
两点,且![]() ,若
,若![]() ,则双曲线的离心率为
,则双曲线的离心率为![]() .
.
其中正确的命题序号为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,﹣2.5,﹣3观察数轴,B,C两点之间的距离为 ;与点A的距离为3的点表示的数是 ;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2020(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则MM两点表示的数分别是:M: ,N: .
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P ,Q .(用含m,n的式子表示这两个数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com