
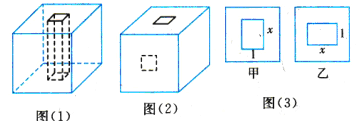
【题目】用橡皮泥做一个棱长为4cm的正方体.
(1)如图(1),在顶面中心位置处从上到下打一个边长为1cm的正方形通孔,打孔后的橡皮泥的表面积是多少?;
(2)如果在第(1)题打孔后,再在正面中心位置处(按图(2)中的虚线)从前到后打一个边长为1cm的正方形通孔,那么打孔后的橡皮泥的表面积为是多少?;
(3)如果把第(2)题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔,能不能使所得橡皮泥的表面积为130cm2?如果能,请求出x;如果不能,请说明理由.
【答案】(1) 110;(2) 118;(3) x=3.
【解析】
(1)打孔后的表面积=原正方体的表面积-小正方形孔的面积+孔中的四个矩形的面积.
(2)打孔后的表面积=图(1)的表面积-4个小正方形孔的面积+新打的孔中的八个小矩形的面积
(3)分两种情形分别列出方程求解即可.
解:(1)表面积S1=96-2+4×4=110(cm2);
故答案为110.
(2)表面积S2=S1-4+4×1.5×2=118(cm2);
故答案为118.(3)能使橡皮泥块的表面积为130cm2,理由为:
①如图甲通孔,由题意,96-2-2(4-x)+3(2+2x)=130,
方程无解,不合题意.
②如图乙通孔,由题意,96-2-2x+4×3+4(2+2x)-2=130,
解得x=3,
∴当边长改为3cm时,表面积为130cm2.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
【答案】3或6
【解析】试题分析:
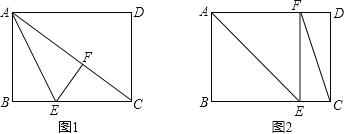
由题意可知有两种情况,见图1与图2;
图1:当点F在对角线AC上时,∠EFC=90°,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=8,
∴BC=AD=8,
在Rt△ABC中,AC=![]() =10,
=10,
设BE=x,则CE=BC﹣BE=8﹣x,
由翻折的性质得,AF=AB=6,EF=BE=x,
∴CF=AC﹣AF=10﹣6=4,
在Rt△CEF中,EF2+CF2=CE2,
即x2+42=(8﹣x)2,
解得x=3,
即BE=3;
图2:当点F落在AD边上时,∠CEF=90°,
由翻折的性质得,∠AEB=∠AEF=![]() ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=6,
综上所述,BE的长为3或6.
故答案为:3或6.
考点:1、轴对称(翻折变换);2、勾股定理
【题型】填空题
【结束】
15
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为7cm,宽为5cm的矩形纸片上,现在剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的的高为_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
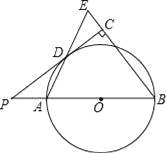
【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=![]()
![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
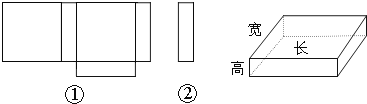
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理绘制成下面的统计图(图1,图2).

小明发现每月每户的用水量在5m3-35m3之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变,根据小明绘制的图表和发现的信息,完成下列问题:
(Ⅰ)n= ,小明调查了 户居民,并补全图2;
(Ⅱ)每月每户用水量的中位数和众数分别落在什么范围?
(Ⅲ)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com