
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
【答案】3或6
【解析】试题分析:
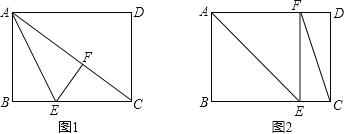
由题意可知有两种情况,见图1与图2;
图1:当点F在对角线AC上时,∠EFC=90°,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=8,
∴BC=AD=8,
在Rt△ABC中,AC=![]() =10,
=10,
设BE=x,则CE=BC﹣BE=8﹣x,
由翻折的性质得,AF=AB=6,EF=BE=x,
∴CF=AC﹣AF=10﹣6=4,
在Rt△CEF中,EF2+CF2=CE2,
即x2+42=(8﹣x)2,
解得x=3,
即BE=3;
图2:当点F落在AD边上时,∠CEF=90°,
由翻折的性质得,∠AEB=∠AEF=![]() ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=6,
综上所述,BE的长为3或6.
故答案为:3或6.
考点:1、轴对称(翻折变换);2、勾股定理
【题型】填空题
【结束】
15
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
科目:初中数学 来源: 题型:
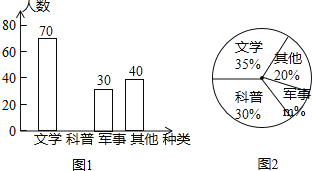
【题目】某学校在开展“书香校园”活动期间,对学生课外阅读的喜好进行抽样调查(每人只选一种书籍),将调查结果绘制成如图所示的两幅不完整的统计图,根据图中的信息,解答下列问题:
(1)这次调查的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;
(3)如果这所学校要添置学生课外阅读的书籍1500册,请你估计“科普”类书籍应添置多少册比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲口袋中装有两个相同的小球,它们的标号分别为2和7,乙口袋中装有两个相同的小球,它们的标号分别为4和5,丙口袋中装有三个相同的小球,它们的标号分别为3,8,9.从这3个口袋中各随机地取出1个小球.
(1)求取出的3个小球的标号全是奇数的概率是多少?
(2)以取出的三个小球的标号分别表示三条线段的长度,求这些线段能构成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在点B的左边,线段AB的长为20cm;点C在点D的左边,点C、D在线段AB上,CD=10cm,点E是线段AC的中点,点F是线段BD的中点
(1)若AC=4cm,求线段EF的长;
(2)若AC=acm,![]() ,用含a的式子表示线段BF的长
,用含a的式子表示线段BF的长
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 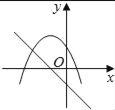 B.
B. 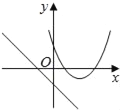 C.
C. 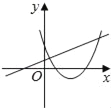 D.
D. 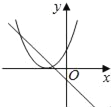
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
【题目】如图,已知菱形ABCD的周长为16,面积为![]() ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
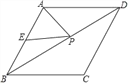
A. 2 B. 2![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=![]() .
.
(1)求证:AMMB=EMMC;
(2)求EM的长;
(3)求sin∠EOB的值.
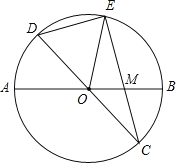
【答案】(1)证明见解析(2)4(3)![]()
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为![]() ,
,
去分母,得![]() .(____________________)
.(____________________)
去括号,得![]() .(____________________)
.(____________________)
移项,得![]() .(____________________)
.(____________________)
合并,得![]() .(合并同类项)
.(合并同类项)
(______),得![]() .(______________)
.(______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
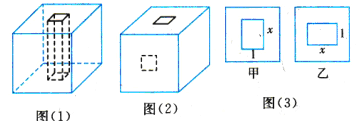
【题目】用橡皮泥做一个棱长为4cm的正方体.
(1)如图(1),在顶面中心位置处从上到下打一个边长为1cm的正方形通孔,打孔后的橡皮泥的表面积是多少?;
(2)如果在第(1)题打孔后,再在正面中心位置处(按图(2)中的虚线)从前到后打一个边长为1cm的正方形通孔,那么打孔后的橡皮泥的表面积为是多少?;
(3)如果把第(2)题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔,能不能使所得橡皮泥的表面积为130cm2?如果能,请求出x;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com