练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．若BF=12，AB=10，则AE的长为（　　）

    A. 10 B. 12 C. 16 D. 18

    【答案】C

    【解析】

    先证明四边形ABEF是菱形，得出AE⊥BF，OA=OE，OB=OF=BF=6，由勾股定理求出OA，即可得出AE的长

    如图，

    ∵四边形ABCD是平行四边形，

    ∴AD∥BC，

    ∴∠DAE=∠AEB，

    ∵∠BAD的平分线交BC于点E，

    ∴∠DAE=∠BEA，

    ∴∠BAE=∠BEA，

    ∴AB=BE，同理可得AB=AF，

    ∴AF=BE，

    ∴四边形ABEF是平行四边形，

    ∵AB=AF，

    ∴四边形ABEF是菱形，

    AE⊥BF，OA=OE，OB=OF=BF=6，

    ∴OA==8，

    ∴AE=2OA=16；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】国家环保局统一规定，空气质量分为5级：当空气污染指数达0—50时为1级，质量为优；51—100时为2级，质量为良；101—200时为3级，轻度污染；201—300时为4级，中度污染；300以上时为5级，重度污染．某城市随机抽取了2015年某些天的空气质量检测结果，并整理绘制成如下两幅不完整的统计图．请根据图中信息，解答下列各题：

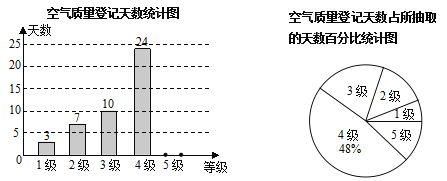
    (1) 本次调查共抽取了 天的空气质量检测结果进行统计；

    (2) 补全条形统计图；

    (3) 扇形统计图中3级空气质量所对应的圆心角为 °；

    (4) 如果空气污染达到中度污染或者以上，将不适宜进行户外活动，根据目前的统计，请你估计2015年该城市有多少天不适宜开展户外活动．(2015年共365天)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

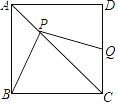
    【题目】如图，正方形，点为对角线上一个动点，为边上一点，且．

    （1）求证：；

    （2）若四边形的面积为25，试探求与满足的数量关系式；

    （3）若为射线上的点，设，四边形的周长为，且，求与的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上两点A、B对应的数分别为－30、0．若点A、B同时出发，点A以每秒2个单位长度的速度向右运动；点B以每秒3个单位长度的速度向左运动，到达点A出发时的位置后立即以每秒4个单位长度的速度向右运动．设运动的时间为t秒．

    （1）求点A和点B第一次相遇时t的值；

    （2）当点A和点B之间的距离为6个单位长度时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

    【答案】3或6

    【解析】试题分析：

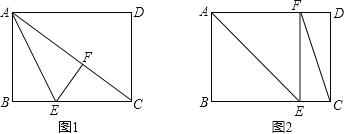
    由题意可知有两种情况，见图1与图2；

    图1：当点F在对角线AC上时，∠EFC=90°，

    ∵∠AFE=∠B=90°，∠EFC=90°，

    ∴点A、F、C共线，

    ∵矩形ABCD的边AD=8，

    ∴BC=AD=8，

    在Rt△ABC中，AC==10，

    设BE=x，则CE=BC﹣BE=8﹣x，

    由翻折的性质得，AF=AB=6，EF=BE=x，

    ∴CF=AC﹣AF=10﹣6=4，

    在Rt△CEF中，EF2+CF2=CE2，

    即x2+42=（8﹣x）2，

    解得x=3，

    即BE=3；

    图2：当点F落在AD边上时，∠CEF=90°，

    由翻折的性质得，∠AEB=∠AEF=×90°=45°，

    ∴四边形ABEF是正方形，

    ∴BE=AB=6，

    综上所述，BE的长为3或6．

    故答案为：3或6．

    考点：1、轴对称（翻折变换）；2、勾股定理

    【题型】填空题
    【结束】
    15

    【题目】计算：()﹣2﹣+（﹣4）0﹣cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

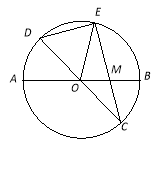
    【题目】已知：如图，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连结DE，DE＝．

    （1）求证：；

    （2）求EM的长；

    （3）求sin∠EOB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于任意四个有理数a，b，c，d，可以组成两个有理数对（a，b）与（c，d）．我们规定：

    （a，b）★（c，d）=bc－ad．

    例如：（1，2）★（3，4）=2×3－1×4=2．

    根据上述规定解决下列问题：

    （1）有理数对（2，－3）★（3，－2）=_______；

    （2）若有理数对（－3，2x－1）★（1，x+1）=7，则x=_______；

    （3）当满足等式（－3，2x－1）★（k，x＋k）=5＋2k的x是整数时，求整数k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

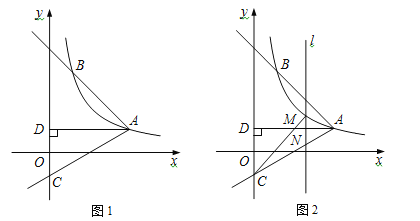
    【题目】如图1，反比例函数（x＞0）的图象经过点A（，1），射线AB与反比例函数图象交于另一点B（1，a），射线AC与y轴交于点C，∠BAC＝75°，AD⊥y轴，垂足为D．

    （1）求k的值；

    （2）求tan∠DAC的值及直线AC的解析式；

    （3）如图2，M是线段AC上方反比例函数图象上一动点，过M作直线l⊥x轴，与AC相交于点N，连接CM，求△CMN面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

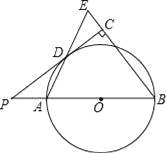
    【题目】如下图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．

    （1）求证：AB=BE；

    （2）若PA=2，cosB=，求⊙O半径的长．

    查看答案和解析>>

    同步练习册答案