
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=![]() .
.
(1)求证:AMMB=EMMC;
(2)求EM的长;
(3)求sin∠EOB的值.
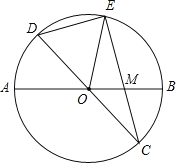
【答案】(1)证明见解析(2)4(3)![]()
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

【答案】(1)见解析;(2)45°;(3)![]()
【解析】试题分析:(1)根据参加生态环保的人数以及百分比求得总人数,用总人数乘以“社区服务”百分比求得其人数,即可解决问题;
(2)根据圆心角=360°×百分比,计算即可;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加同一服务活动的情况,再利用概率公式求解即可求得答案.
试题解析:(1)该班全部人数:12÷25%=48人.
社区服务的人数为48×50%=24,
补全折线统计如图所示:
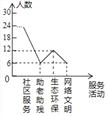
(2)网络文明部分对应的圆心角的度数为360°×![]() =45°;
=45°;
(3)分别用A,B,C,D表示“社区服务、助老助残、生态环保、网络文明”四个服务活动,
画树状图得:
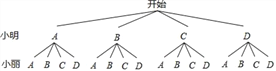
∵共有16种等可能的结果,他们参加同一服务活动的有4种情况,
∴他们参加同一服务活动的概率为![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
【答案】3或6
【解析】试题分析:
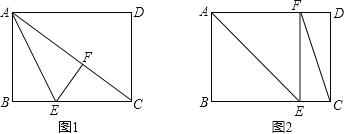
由题意可知有两种情况,见图1与图2;
图1:当点F在对角线AC上时,∠EFC=90°,
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=8,
∴BC=AD=8,
在Rt△ABC中,AC=![]() =10,
=10,
设BE=x,则CE=BC﹣BE=8﹣x,
由翻折的性质得,AF=AB=6,EF=BE=x,
∴CF=AC﹣AF=10﹣6=4,
在Rt△CEF中,EF2+CF2=CE2,
即x2+42=(8﹣x)2,
解得x=3,
即BE=3;
图2:当点F落在AD边上时,∠CEF=90°,
由翻折的性质得,∠AEB=∠AEF=![]() ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=6,
综上所述,BE的长为3或6.
故答案为:3或6.
考点:1、轴对称(翻折变换);2、勾股定理
【题型】填空题
【结束】
15
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ;当t=3时,OP=
(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时追上点P?
(3)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时PR相距2个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
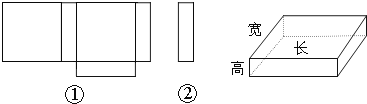
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com