
【题目】如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4![]() ,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于_____.
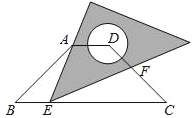
【答案】2,4![]() ﹣3,
﹣3,![]()
【解析】分析:首先理解题意,得出此题应该分三种情况进行分析,分别是AB=AE,AB=BE,AE=BE,从而得到最后答案.
详解:作AM⊥BC,DN⊥BC,
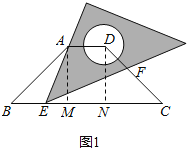
根据已知条件可得,BM=(BC-AD)÷2,
在直角三角形ABM中,cosB=![]() ,
,
则AB=(BC-AD)÷2÷cosB=3,
①当AB=AE′时,如图,
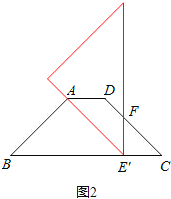
∠B=45°,∠AE′B=45°,
∴AE′=AB=3,
则在Rt△ABE′中,BE′=![]() ,
,
故E′C=4![]() -3
-3![]() =
=![]() .
.
易得△FE′C为等腰直角三角形,
故CF=![]() =2.
=2.
②当AB=BE″时,
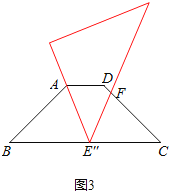
∵AB=3,
∴BE″=3,
∵∠AE″B=∠BAE″=(180°-45°)÷2=67.5°,
∴∠FE″C=180°-45°-67.5°=67.5°,
∴∠CFE″=180°-∠C-∠FE″C=67.5°,
∵△E″CF为等腰三角形,
∴CF=CE″=CB-BE″=4![]() -3;
-3;
③当AE=BE′″时,△ABE′″和△CFE′″是等腰Rt△,
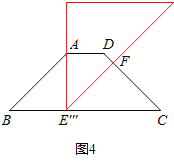
∴BE′″=![]() ,
,
∴CE′″=![]()
∴CF=FE′″=![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
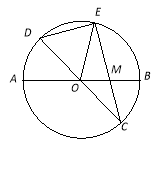
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
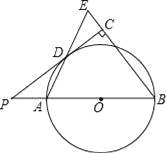
【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=![]()
![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a-b|,线段AB的中点表示的数为![]()
![]()
(问题情境)如图1,已知数轴上有三点![]() 、
、![]() 、
、![]() ,
,![]() ,点
,点![]() 对应的数是
对应的数是![]() .
.
(综合运用)(1)点B表示的数是__________.
(2)若![]() ,求点
,求点![]() 到原点的距离.
到原点的距离.
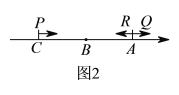
(3)如图2,在(2)的条件下,动点![]() 、
、![]() 两点同时从
两点同时从![]() 、
、![]() 出发向右运动,同时动点
出发向右运动,同时动点![]() 从点
从点![]() 向左运动,已知点
向左运动,已知点![]() 的速度是点
的速度是点![]() 的速度的
的速度的![]() 倍,点
倍,点![]() 的速度是点
的速度是点![]() 的速度
的速度![]() 倍少
倍少![]() 个单位长度/秒.经过
个单位长度/秒.经过![]() 秒,点
秒,点![]() 、
、![]() 之间的距离与点
之间的距离与点![]() 、
、![]() 之间的距离相等,求动点
之间的距离相等,求动点![]() 的速度;
的速度;
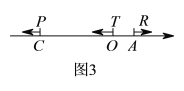
(4)如图3,在(2)的条件下,![]() 表示原点,动点
表示原点,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发向左运动,同时动点
两点同时出发向左运动,同时动点![]() 从点
从点![]() 出发向右运动,点
出发向右运动,点![]() 、
、![]() 、
、![]() 的速度分别为
的速度分别为![]() 个单位长度/秒,
个单位长度/秒,![]() 个单位长度/秒、
个单位长度/秒、![]() 个单位长度/秒,在运动过程中,如果点
个单位长度/秒,在运动过程中,如果点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.请问
的中点.请问![]() 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
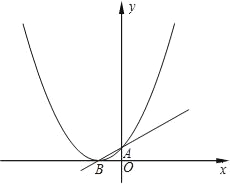
【题目】已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
(1)求这个函数关系式;
(2)如图所示,设二次函数y=ax2+x+1图象的顶点为B,与y轴的交点为A,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;
(3)在(2)中,若圆与x轴另一交点关于直线PB的对称点为M,试探索点M是否在抛物线y=ax2+x+1上?若在抛物线上,求出M点的坐标;若不在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道,![]() 它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子
它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子![]() ,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=
,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=![]() .根据
.根据
以上信息,回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5的两点之间的距离是 .
(2)点A、B在数轴上分别表示实数x和![]() .
.
①用代数式表示A、B两点之间的距;
②如果![]() ,求x的值.
,求x的值.
(3)直接写出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com