
����Ŀ��2014��1�£����ҷ���ί��ָ̨�������Ҫ��2015���ǰ�����г���ԭ����ȫ��ʵ�о������ˮ���ƶȣ�С��Ϊ�˽�����������ˮ�۷�������ᷴ�죬����������Լ���ס��С���IJ��־�����ÿ��ÿ������ˮ�����������۶���ˮ��Ϊ�ı�������������е��飬���ѵ����������������ͼ1��ͼ2��

С������ÿ��ÿ������ˮ����5m2-35m2֮�䣬��8���������ˮ�۸�����Ƿ�������ν�����ÿ�����ˮ��ʽ�ĸı䣮����С�����Ƶ�ͼ���ͷ��ֵ���Ϣ������������⣺
��1��n= ��С�������� ��������ȫͼ1��
��2��ÿ��ÿ����ˮ������λ���������ֱ�����ʲô��Χ��
��3�����С�����ڵ�С����1800����������������ӵ����Ƿ���ȡ��Ӧ����ˮ��ʽ�ı����ľ������ж��٣�
���𰸡���1��210 �� 96��(2��15m3-20m3��10m3-15m3��(3��1050��
��������
�⣺��1��n=360-30-120=210��
��8��![]() =96������
=96������
����������96������
ÿ��ÿ������ˮ����15m3-20m3֮��ľ���Ļ����ǣ�
96-��15+22+18+16+5��
=96-76
=20��������
��ͼ���£�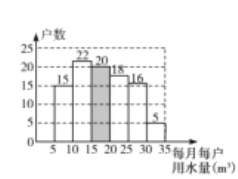
�ʴ�Ϊ��210��96��
��2���߹���96�����ݣ�
��ÿ��ÿ����ˮ������λ��Ϊ��48��49�������ݵ�ƽ����������λ������15m3-20m3��
������ͼ֪��10m3-15m3��������࣬����������10m3-15m3��
�ʴ�Ϊ��15m3-20m3��10m3-15m3��
��3����������ã�
1800��![]() =1050��������
=1050��������
���ӵ����Ƿ���ȡ��Ӧ����ˮ��ʽ�ı����ľ�������1050����


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������A��B��Ӧ�����ֱ�Ϊ��30��0������A��Bͬʱ��������A��ÿ��2����λ���ȵ��ٶ������˶�����B��ÿ��3����λ���ȵ��ٶ������˶��������A����ʱ��λ�ú�������ÿ��4����λ���ȵ��ٶ������˶������˶���ʱ��Ϊt�룮
��1�����A�͵�B��һ������ʱt��ֵ��
��2������A�͵�B֮��ľ���Ϊ6����λ����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������������![]() ��x��0����ͼ����A��
��x��0����ͼ����A��![]() ��1��������AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC��75�㣬AD��y��������ΪD��
��1��������AB�뷴��������ͼ������һ��B��1��a��������AC��y�ύ�ڵ�C����BAC��75�㣬AD��y��������ΪD��
��1����k��ֵ��
��2����tan��DAC��ֵ��ֱ��AC�Ľ���ʽ��
��3����ͼ2��M���߶�AC�Ϸ�����������ͼ����һ��������M��ֱ��l��x������AC�ཻ�ڵ�N������CM�����CMN��������ֵ��
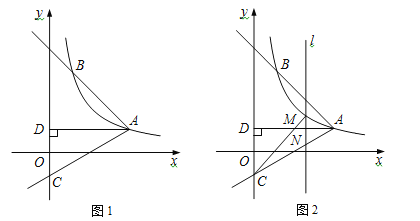
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֽƬABCD����ͼ��ʾ�ķ�ʽ�۵���ǡ�õõ�����AECF����AB��3��������AECF�����Ϊ_____��
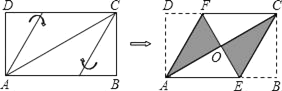
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�Ϊ7cm����Ϊ5cm�ľ���ֽƬ�ϣ����ڼ���һ������Ϊ4cm�ĵ��������Σ�Ҫ����������ε�һ����������ε�һ�������غϣ���������������ھ��εı��ϣ�����µĵ���������һ���ϵĵĸ�Ϊ_____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����֪AB�ǡ�O��ֱ������P��BA���ӳ����ϣ�PD�С�O�ڵ�D������B��BE��ֱ��PD����PD���ӳ����ڵ�C������AD���ӳ�����BE�ڵ�E��
��1����֤��AB=BE��
��2����PA=2��cosB=![]()
![]() �����O�뾶�ij���
�����O�뾶�ij���
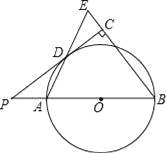
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
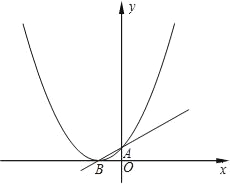
����Ŀ����֪������y=ax2+x+1��ͼ����x��ֻ��һ�������㣮
��1�������������ϵʽ��
��2����ͼ��ʾ������κ���y=ax2+x+1ͼ��Ķ���ΪB����y��Ľ���ΪA��PΪͼ���ϵ�һ�㣬�����߶�PBΪֱ����Բ��ֱ��AB�����ڵ�B����P������ꣻ
��3���ڣ�2���У���Բ��x����һ�������ֱ��PB�ĶԳƵ�ΪM����̽����M�Ƿ���������y=ax2+x+1�ϣ������������ϣ����M������ꣻ�����ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����ݣ�x1��x2��x3��x4��x5��x6��ƽ������2��������3������һ�����ݣ�3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��3x6��2��ƽ�����ͷ���ֱ��ǣ�������
A. 2��3 B. 2��9 C. 4��25 D. 4��27
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com