
【题目】(2017黑龙江省龙东地区)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
(1)如图1所示,易证:OH=![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
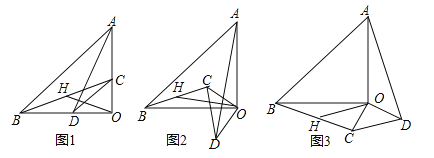
【答案】(1)证明见解析;(2)图2,图3的结论都相同:OH=![]() AD,OH⊥AD.
AD,OH⊥AD.
【解析】试题(1)只要证明△AOD≌△BOC,即可解决问题;
(2)①如图2中,结论:OH=![]() AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,由△BEO≌△ODA即可解决问题;
AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,由△BEO≌△ODA即可解决问题;
②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.由△BEO≌△ODA即可解决问题;
试题解析:(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,∴OC=OD,OA=OB,在△AOD与△BOC中,∵OA=OB,∠AOD=∠BOC,OD=OC,∴△AOD≌△BOC(SAS),∴∠ADO=∠BCO,∠OAD=∠OBC,∵点H为线段BC的中点,∴OH=HB,∴∠OBH=∠HOB=∠OAD,又∵∠OAD+∠ADO=90°,∴∠ADO+∠BOH=90°,∴OH⊥AD;
(2)解:①结论:OH=![]() AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,易证△BEO≌△ODA,∴OE=AD,∴OH=
AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,易证△BEO≌△ODA,∴OE=AD,∴OH=![]() OE=
OE=![]() AD.由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOH=∠EOB+∠AOH=90°,∴OH⊥AD.
AD.由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOH=∠EOB+∠AOH=90°,∴OH⊥AD.
②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA,∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOF=∠EOB+∠AOG=90°,∴∠AGO=90°,∴OH⊥AD.


科目:初中数学 来源: 题型:
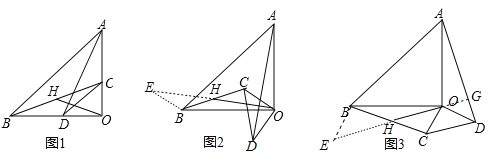
【题目】已知:函数y=ax2+x+1的图象与x轴只有一个公共点.
(1)求这个函数关系式;
(2)如图所示,设二次函数y=ax2+x+1图象的顶点为B,与y轴的交点为A,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;
(3)在(2)中,若圆与x轴另一交点关于直线PB的对称点为M,试探索点M是否在抛物线y=ax2+x+1上?若在抛物线上,求出M点的坐标;若不在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据:x1,x2,x3,x4,x5,x6的平均数是2,方差是3,则另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,3 B. 2,9 C. 4,25 D. 4,27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说明理由
如图,∠1+∠2=230°,b∥c, 则∠1、∠2、∠3、∠4各是多少度?
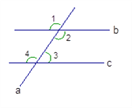
解:∵ ∠1=∠2 (_________________________)
∠1+∠2=230°
∴∠1 =∠2 =________(填度数)
∵ b∥c
∴∠4 =∠2= ________(填度数)
( )
∠2 +∠3 =180° ( )
∴∠3 =180°-∠2 =_________(填度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,给出以下判断:①四边形
,给出以下判断:①四边形![]() 是菱形;②四边形
是菱形;②四边形![]() 的面积
的面积![]() ;③顺次连接四边形
;③顺次连接四边形![]() 的四边中点得到的四边形是正方形;④将
的四边中点得到的四边形是正方形;④将![]() 沿直线
沿直线![]() 对折,点
对折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,当
,当![]() 时,点
时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;其中真确的是( )
;其中真确的是( )
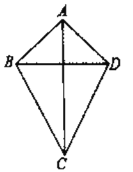
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
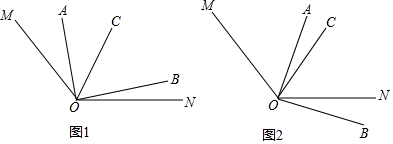
(1)在图1中,若∠AOC=40°,则∠BOC= °,∠NOB= °.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系( 必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:
![]() ,0,5.2,
,0,5.2, ![]() ,+(﹣4),﹣2
,+(﹣4),﹣2![]() ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…
(1)分数集合:{______ …}
(2)非负整数集合:{______ …}
(3)有理数集合:{______ …}.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com