
【题目】已知,抛物线y=ax2﹣![]() ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
(1)求这条抛物线的解析式及直线BC的解析式;
(2)设点D为抛物线对称轴上的一点,当点D在对称轴上运动时,是否可以与点C,A,B三点,构成梯形的四个顶点?若可以,求出点D坐标,若不可以,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2,y=
x﹣2,y=![]() x﹣2;(2)见解析
x﹣2;(2)见解析
【解析】分析:(1)将函数解析式变形为y=a(x-2![]() )(x+
)(x+![]() )可得A、B坐标,由解析式知C(0,-4a),根据△AOC∽△COB知
)可得A、B坐标,由解析式知C(0,-4a),根据△AOC∽△COB知![]() ,据此求得a的值,进一步可得抛物线和直线BC解析式;
,据此求得a的值,进一步可得抛物线和直线BC解析式;
(2)分CD1∥AB、AD2∥BC、BD3∥AC三种情况,利用相似三角形的性质分别求解可得答案.
详解:(1)∵y=ax2﹣![]() x﹣4a=a(x﹣2
x﹣4a=a(x﹣2![]() )(x+
)(x+![]() ),
),
∴由a(x﹣2![]() )(x+
)(x+![]() )=0且a≠0可得x=2
)=0且a≠0可得x=2![]() 或x=
或x=![]() ,
,
由题意知点A(﹣![]() ,0)、B(2
,0)、B(2![]() ,0),
,0),
当x=0时,y=﹣4a,
∴点C(0,﹣4a),
∵C点在x轴下方,
∴﹣4a<0,a>0,
如图1所示,
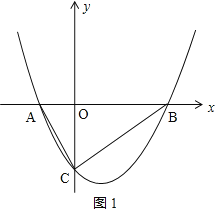
∵△AOC∽△COB,
∴![]() ,即
,即![]() ,
,
解得:a=﹣![]() (舍)或a=
(舍)或a=![]() ,
,
则抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣2,点C坐标为(0,﹣2),
x﹣2,点C坐标为(0,﹣2),
设直线BC解析式为y=kx+b,
将B(2![]() ,0)、C(0,﹣2)代入,得:
,0)、C(0,﹣2)代入,得:![]() ,
,
解得: ,
,
∴直线BC解析式为y=![]() x﹣2;
x﹣2;
(2)抛物线的对称轴为x=![]() ,
,
①如图2,当CD1∥AB时,四边形ACD1B为梯形,
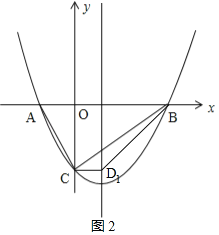
∵点C(0,﹣2),
∴点D1坐标为(![]() ,﹣2);
,﹣2);
②如图3,当AD2∥BC时,四边形ACBD2为梯形,

∴∠D2AE=∠CBO,
∵∠AED2=∠BOC=90°,
∴△AD2E∽△BOC,
∴![]() ,即
,即![]() ,
,
解得:D2E=![]() ,
,
∴点D2坐标为(![]() ,
,![]() );
);
③如图4,当BD3∥AC时,四边形ACBD3为梯形,
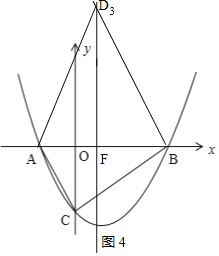
∴∠OAC=∠FBD3,
∵∠AOC=∠BFD3=90°,
∴△AOC∽△BFD3,
∴![]() ,即
,即![]() ,
,
解得:FD3=3,
∴点D3的坐标为(![]() ,3);
,3);
综上,点D的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,
,![]() )或(
)或(![]() ,3).
,3).


科目:初中数学 来源: 题型:
【题目】已知一组数据:x1,x2,x3,x4,x5,x6的平均数是2,方差是3,则另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,3 B. 2,9 C. 4,25 D. 4,27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB,
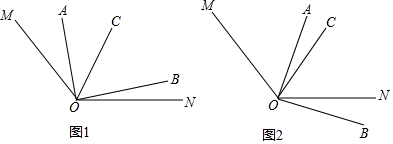
(1)在图1中,若∠AOC=40°,则∠BOC= °,∠NOB= °.
(2)在图1中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系( 必须写出推理的主要过程,但每一步后面不必写出理由);
(3)在已知条件不变的前提下,当∠AOB绕着点O顺时针转动到如图2的位置,此时α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入它所属的集合内:
![]() ,0,5.2,
,0,5.2, ![]() ,+(﹣4),﹣2
,+(﹣4),﹣2![]() ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…
(1)分数集合:{______ …}
(2)非负整数集合:{______ …}
(3)有理数集合:{______ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
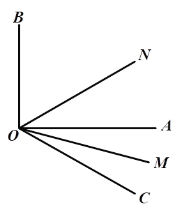
【题目】如图∠AOB是直角,在∠AOB外作射线OC,OM平分∠AOC,ON平分∠BOC.
(1)若∠AOC=38°,求∠MON的度数;
(2)若∠AOC=![]() ,试说明∠MON的大小与
,试说明∠MON的大小与![]() 无关.
无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
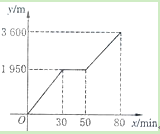
【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t s.
(1)当点B与点C相遇时,点A、点D在数轴上表示的数分别为________;
(2)当t为何值时,点B刚好与线段CD的中点重合;
(3)当运动到BC=8(单位长度)时,求出此时点B在数轴上表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种关于整数n的“F”运算:
(1)当n是奇数时,结果为![]() ;
;
(2)当n是偶数时,结果是![]() (其中
(其中![]() 是使
是使![]() 是奇数的正整数),并且运算重复进行.
是奇数的正整数),并且运算重复进行.
例如:取![]() ,第一次经F运算是29,第二次经F运算是92,第三次经F运算是23,第四次经F运算是74…;若
,第一次经F运算是29,第二次经F运算是92,第三次经F运算是23,第四次经F运算是74…;若![]() ,则第2019次运算结果是________
,则第2019次运算结果是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com