练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】定义一种关于整数n的“F”运算：

    （1）当n是奇数时，结果为；

    （2）当n是偶数时，结果是（其中是使是奇数的正整数），并且运算重复进行．

    例如：取，第一次经F运算是29，第二次经F运算是92，第三次经F运算是23，第四次经F运算是74…；若，则第2019次运算结果是________

    【答案】1

    【解析】

    根据整数n的“F”运算的定义可发现：若，第一次经F运算是，第二次经F运算是，第三次经F运算是，第四次经F运算是，第五次经F运算是，第六次经F运算是……可发现以后的运算结果都是1、8循环，从而可求第2019次运算结果.

    解：若，第一次经F运算是，第二次经F运算是，第三次经F运算是，第四次经F运算是，第五次经F运算是，第六次经F运算是……

    （2019－2）÷2=1008……1

    第2019次运算结果是：1.

    故答案为：1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，抛物线y=ax2﹣ax﹣4a与x轴交于A，B两点，与y轴交于C点，A点在B点左侧，C点在x轴下方，且△AOC∽△COB

    （1）求这条抛物线的解析式及直线BC的解析式；

    （2）设点D为抛物线对称轴上的一点，当点D在对称轴上运动时，是否可以与点C，A，B三点，构成梯形的四个顶点？若可以，求出点D坐标，若不可以，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

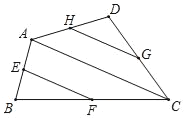
    【题目】如图，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点．

    （1）如果图中线段都可画成有向线段，那么在这些有向线段所表示的向量中，与向量相等的向量是　 　；

    （2）设＝，＝，＝．试用向量，或表示下列向量：＝　 　；＝　 　．

    （3）求作：．（请在原图上作图，不要求写作法，但要写出结论）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于反比例函数，下列说法中不正确的是（ ）

    A. x>0时，y随x增大而增大

    B. 图像分布在第二第四象限

    C. 图像经过点（1.-2）

    D. 若点A（）B（）在图像上，若,则

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．

    （1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是 ；

    （2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

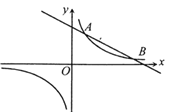
    【题目】如图，反比例函数y=的图象与一次函数y=kx+b的图象交于A，B两点，点A的坐标为（2，6），点B的坐标为（n，1）．

    （1）求反比例函数与一次函数的表达式；

    （2）点E为y轴上一个动点，若S△AEB=10，求点E的坐标．

    （3）结合图像写出不等式的解集；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，平分，交于点，交的延长线于点，交于点．

    （1）求证：四边形为菱形；

    （2）若，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

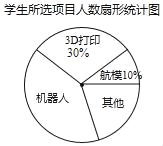
    【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．

    男、女生所选项目人数统计表

    项目

    男生（人数）

    女生（人数）

    机器人

    7

    9

    3D打印

    m

    4

    航模

    2

    2

    其他

    5

    n

    根据以上信息解决下列问题：

    （1）m=_____，n=_____；

    （2）扇形统计图中机器人项目所对应扇形的圆心角度数为_____°；

    （3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

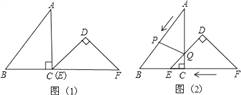
    【题目】已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上，∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm．如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿BA匀速移动，当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动，DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．

    解答下列问题：

    （1）当t为何值时，点A在线段PQ的垂直平分线上？

    （2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式，是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由；

    （3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案