
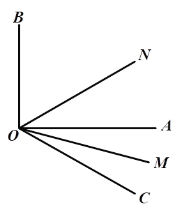
【题目】如图∠AOB是直角,在∠AOB外作射线OC,OM平分∠AOC,ON平分∠BOC.
(1)若∠AOC=38°,求∠MON的度数;
(2)若∠AOC=![]() ,试说明∠MON的大小与
,试说明∠MON的大小与![]() 无关.
无关.
【答案】(1)45°;(2)见解析.
【解析】
(1)先求出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解;
(2)根据(1)的思路,先用含![]() 的式子表示出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解.
的式子表示出∠BOC,再根据角平分线的定义求出∠COM、∠CON,然后根据∠MON=∠CON-∠COM,代入数据进行计算即可得解.
解:(1)∵∠AOB是直角,∠AOC=38°,
∴∠BOC=∠AOB+∠AOC=90°+38°=128°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠COM= ![]() ∠AOC=
∠AOC= ![]() ×38°=19°,
×38°=19°,
∠CON= ![]() ∠BOC=
∠BOC= ![]() ×128°=64°,
×128°=64°,
∴∠MON=∠CON-∠COM,
=64°-19°,
=45°;
(2)∵∠AOB是直角,∠AOC=α,
∴∠BOC=∠AOB+∠AOC=90°+α,
∵OM平分∠AOC,ON平分∠BOC,
∴∠COM= ![]() ∠AOC=
∠AOC= ![]() α,
α,
∠CON= ![]() ∠BOC=
∠BOC= ![]() (90°+α)=45°+
(90°+α)=45°+ ![]() α,
α,
∴∠MON=45°+ ![]() α-
α- ![]() α=45°;
α=45°;
故∠MON的大小与α无关.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动到点A停止,设点P运动路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则矩形ABCD的面积是( )
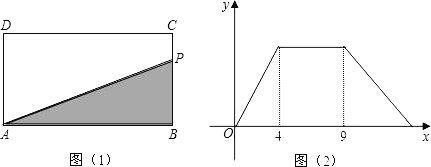
A. 10B. 16C. 20D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一种零件的直径的合格情况,随机各抽取了10个样品进行检测,已知零件的直径均为整数,整理数据如下:(单位:![]() )
)
170~174 | 175~179 | 180~184 | 185~189 | |
甲车间 | 1 | 3 | 4 | 2 |
乙车间 | 0 | 6 | 2 | 2 |
(1)分别计算甲、乙两车间生产的零件直径的平均数;
(2)直接说出甲、乙两车间生产的零件直径的中位数都在哪个小组内,众数是否在其相应的小组内?
(3)若该零件的直径在![]() 的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
的范围内为合格,甲、乙两车间哪一个车间生产的零件直径合格率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
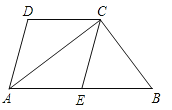
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”已成为推动课堂教学改革,打造自主高效课堂的重要措施.某中学从全校学生中随机抽取部分学生对“分组合作学习”实施后的学习兴趣情况进行调查分析,统计图如下:

请结合图中信息解答下列问题:
(1)求出随机抽取调查的学生人数;
(2)补全分组后学生学习兴趣的条形统计图;
(3)分组后学生学习兴趣为“中”的所占的百分比和对应扇形的圆心角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2﹣![]() ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
(1)求这条抛物线的解析式及直线BC的解析式;
(2)设点D为抛物线对称轴上的一点,当点D在对称轴上运动时,是否可以与点C,A,B三点,构成梯形的四个顶点?若可以,求出点D坐标,若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分∠BCE.

查看答案和解析>>
科目:初中数学 来源: 题型:
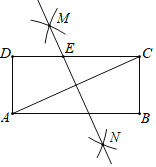
【题目】如图,在矩形ABCD中,按以下步骤作图:①分别以点A和点C为圆心,以大于![]() AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=_____________.
AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E,若AB=8,AD=6,则EC=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com