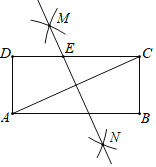
【题目】如图，在矩形ABCD中，按以下步骤作图：①分别以点A和点C为圆心，以大于
AC的长为半径作弧，两弧相交于点M和N；②作直线MN交CD于点E，若AB=8，AD=6，则EC=_____________．
科目：初中数学 来源： 题型：
【题目】说明理由
如图，∠1＋∠2＝230°，b∥c， 则∠1、∠2、∠3、∠4各是多少度？
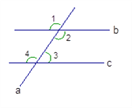
解：∵ ∠1＝∠2 (_________________________)
∠1＋∠2＝230°
∴∠1 ＝∠2 ＝________（填度数）
∵ b∥c
∴∠4 ＝∠2＝ ________（填度数）
( )
∠2 ＋∠3 ＝180° ( )
∴∠3 ＝180°－∠2 ＝_________（填度数）
查看答案和解析>>
科目：初中数学 来源： 题型：
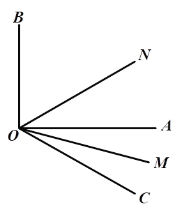
【题目】如图∠AOB是直角，在∠AOB外作射线OC，OM平分∠AOC，ON平分∠BOC.
(1)若∠AOC=38°，求∠MON的度数；
(2)若∠AOC=
，试说明∠MON的大小与无关.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴上线段AB＝2(单位长度)，线段CD＝4(单位长度)，点A在数轴上表示的数是－10，点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动，同时线段CD以每秒2个单位长度的速度向左匀速运动．设运动时间为t s.
(1)当点B与点C相遇时，点A、点D在数轴上表示的数分别为________；
(2)当t为何值时，点B刚好与线段CD的中点重合；
(3)当运动到BC＝8(单位长度)时，求出此时点B在数轴上表示的数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某电路检修小组在东西方向的一道路上检修用电线路，检修车辆从该道路
处出发，如果规定检修车辆向东行驶为正，向西行驶为负，某一天施工过程中七次车辆行驶记录如下（单位：千米）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
（
）问检修小组收工时在的哪个方位？距处多远？
（2）若检修车辆每千米耗油
升，每升汽油需
元，问这一天检修车辆所需汽油费多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】知识链接：
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法，通过“转化、化归”通常可以实现化未知为已知，化复杂为简单，从而使问题得以解决.
（1）问题背景：已知：△ABC.试说明：∠A+∠B+∠C=180°.
问题解决：（填出依据）
解：（1）如图①，延长AB到E，过点B作BF∥AC.
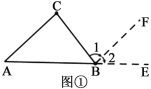
∵BF∥AC（作图）
∴∠1=∠C（ ）
∠2=∠A（ ）
∵∠2+∠ABC+∠1=180°（平角的定义）
∴∠A+∠ABC+∠C=180°（等量代换）
小结反思：本题通过添加适当的辅助线，把三角形的三个角之和转化成了一个平角，利用平角的定义，说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
（2）类比探究：请同学们参考图②，模仿（1）的解决过程试说明“三角形的三个内角和等于180°”
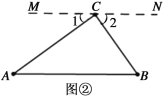
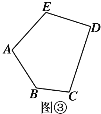
（3）拓展探究：如图③，是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC中，∠ACB＝90°，D是边BC上一点，点E、F分别是线段AB、AD中点，联结CE、CF、EF．
（1）求证：△CEF≌△AEF；
（2）联结DE，当BD＝2CD时，求证：AD＝2DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】实验数据显示，一般成人喝半斤低度白酒后，1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数y＝－200x2＋400x刻画；1.5时后(包括1.5时)y与x可近似地用反比例函数
(k＞0)刻画(如图所示)．
（1）根据上述数学模型计算：喝酒后几时血液中的酒精含量达到最大值？最大值为多少
（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：30在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
