
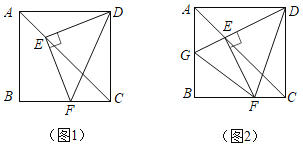
【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
【答案】(1)45°;(2)GF=AG+CF,证明见解析;(3)①6; ②![]() ,理由见解析.
,理由见解析.
【解析】
(1)如图1中,连接BE.利用全等三角形的性质证明EB=ED,再利用等角对等边证明EB=EF即可解决问题.
(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,证明△GDH≌△GDF(SAS)即可解决问题.
(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,利用勾股定理构建方程求出x即可.
②设正方形边长为x,利用勾股定理构建关系式,利用整体代入的思想解决问题即可.
解:(1)如图1中,连接BE.
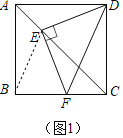
∵四边形ABCD是正方形,
∴CD=CB,∠ECD=∠ECB=45°,
∵EC=EC,
∴△ECB≌△ECD(SAS),
∴EB=ED,∠EBC=∠EDC,
∵∠DEF=∠DCF=90°,
∴∠EFC+∠EDC=180°,
∵∠EFB+∠EFC=180°,
∴∠EFB=∠EDC,
∴∠EBF=∠EFB,
∴EB=EF,
∴DE=EF,
∵∠DEF=90°,
∴∠EDF=45°
故答案为45°.
(2)猜想:GF=AG+CF.
如图2中,将△CDF绕点D旋转90°,得△ADH,
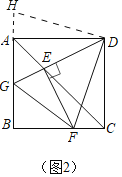
∴∠CDF=∠ADH,DF=DH,CF=AH,∠DAH=∠DCF=90°,
∵∠DAC=90°,
∴∠DAC+∠DAH=180°,
∴H、A、G三点共线,
∴GH=AG+AH=AG+CF,
∵∠EDF=45°,
∴∠CDF+∠ADG=45°,
∴∠ADH+∠ADG=45°
∴∠GDH=∠EDF=45°
又∵DG=DG
∴△GDH≌△GDF(SAS)
∴GH=GF,
∴GF=AG+CF.
(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,
则有(3+x)2=(6-x)2+32,
解得x=2
∴S△BFG=![]() BFBG=6.
BFBG=6.
②设正方形边长为x,
∵AG=a,CF=b,
∴BF=x-b,BG=x-a,GF=a+b,
则有(x-a)2+(x-b)2=(a+b)2,
化简得到:x2-ax-bx=ab,
∴S=![]() (x-a)(x-b)=
(x-a)(x-b)=![]() (x2-ax-bx+ab)=
(x2-ax-bx+ab)=![]() ×2ab=ab.
×2ab=ab.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
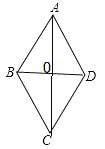
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
【答案】![]()
【解析】分析:根据菱形的性质易得AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,再判定△ABD为等边三角形,根据等边三角形的性质可得AB=BD=8,从而得OB=4,在Rt△AOB中,根据勾股定理可得OA=4![]() ,继而求得AC=2AO=
,继而求得AC=2AO=![]() ,再由菱形的面积公式即可求得菱形ABCD的面积.
,再由菱形的面积公式即可求得菱形ABCD的面积.
详解:∵菱形ABCD中,其周长为32,
∴AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,
∵![]() ,
,
∴△ABD为等边三角形,
∴AB=BD=8,
∴OB=4,
在Rt△AOB中,OB=4,AB=8,
根据勾股定理可得OA=4![]() ,
,
∴AC=2AO=![]() ,
,
∴菱形ABCD的面积为: ![]() =
=![]() .
.
点睛:本题考查了菱形性质:1.菱形的四个边都相等;2.菱形对角线相互垂直平分,并且每一组对角线平分一组对角;3.菱形面积公式=对角线乘积的一半.
【题型】填空题
【结束】
17
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )

A. ![]() cm2 B. 1cm2 C. 2cm2 D. 4cm2
cm2 B. 1cm2 C. 2cm2 D. 4cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,已知线段AB=20cm,在AB上取一点P,M是AB的中点,N是AP中点,若MN=3cm,求线段AP的长;
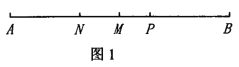
(2)如图2所示,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.则∠COE是多少度?
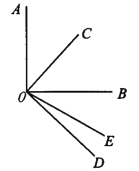
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
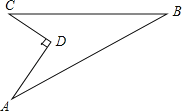
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点 A 在数轴上对应的数为 a,点B在数轴上对应的数为 b,且 a, b 满足|a+1|+(b-11)![]() =0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
=0, 若 P 是线段 AB 上任意一点,C、D 两点分别从点P、B 开始出发,同时向点A运动,如果点 C 的运动速度为2 cm/s,点 D 的运动速度为 3 cm/s,运动的时间为t s .
![]()
(1)求线段 AB 的长;
(2)若 AP=8cm,
①当 C、D 两点运动 1 s 后,求线段 CD 的长;
②当 C、D 两点运动 t s 后,且点 D 在线段 PB 上时,用含t 的代数式表示线段 AC、CD 的长,并说明AC 与 CD 的数量关系.
(3)如果 t=2 s,CD=1 cm,试探索线段 AP 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com