
【题目】福建省教育厅日前发布文件,从2019年开始,体育成绩将按一定的原始分计入中考总分。某校为适应新的中考要求,决定为体育组添置一批体育器材。学校准备在网上订购一批某品牌足球和跳绳,在查阅天猫网店后发现足球每个定价150元,跳绳每条定价30元.现有A、B两家网店均提供包邮服务,并提出了各自的优惠方案.
A网店:买一个足球送一条跳绳;
B网店:足球和跳绳都按定价的90%付款.
已知要购买足球40个,跳绳x条(x>40)
(1)若在A网店购买,需付款 元(用含x的代数式表示).
若在B网店购买,需付款 元(用含x的代数式表示).
(2)若x=100时,通过计算说明此时在哪家网店购买较为合算?
(3)当x=100时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,
并计算需付款多少元?
【答案】(1)(4800+30x),(5400+27x);(2)见解析;(3) 在A网店购买40个足球配送40个跳绳,再在B网店购买60个跳绳,付款7620元.
【解析】
(1)先根据题意列出算式,再化简即可;
(2)把x=100代入(1)中的代数式,求出结果,再比较即可;
(3)比较划算的方方案是:在A网店买40个足球和40个跳绳,在B网店买60个跳绳,求出即可.
解:(1)![]() . 若在A网店购买,需付款150×40+30(x-40)=(30x+4800)元,
. 若在A网店购买,需付款150×40+30(x-40)=(30x+4800)元,
若在B网店购买,需付款150×90%×40+30×90x=(27x+5400)元,
故答案为:27x+5400,27x+5400;
(2)当x=100时
在A网店购买需付款:![]() 元;
元;
在B网店购买需付款:![]() 元.
元.
∵![]()
∴当![]() 时应选择在A网店购买合算.
时应选择在A网店购买合算.
(3)当![]() 时
时
在A网店购买需付款:![]() 元;
元;
在B网店购买需付款:![]() 元.
元.
在A网店购买40个足球配送40个跳绳,再在B网店购买60个跳绳合计需付款:
![]() 元.
元.
∵![]()
∴省钱的购买方案是:
在A网店购买40个足球配送40个跳绳,再在B网店购买60个跳绳,付款![]() 元.
元.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:![]() ________.
________.
(2)填空:
①当![]() 时,代数式
时,代数式![]() ________;
________;
②当![]() ________时,代数式
________时,代数式![]() ;
;
③代数式![]() 的最小值是________.
的最小值是________.
(3)拓展与应用:求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=![]() .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:
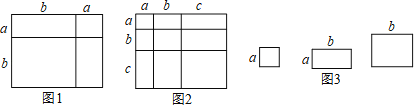
(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 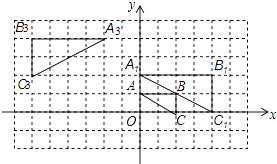
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )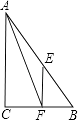
A.△ABC是直角三角形
B.AF是△ABC的中位线
C.EF是△ABC的中位线
D.△BEF的周长为6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com