
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】试题分析:①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;
③先证△BEF是等边三角形得出BF=EF,再证DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.
①∵矩形ABCD中,O为AC中点, ∴OB=OC, ∵∠COB=60°, ∴△OBC是等边三角形, ∴OB=BC,
∵FO=FC, ∴FB垂直平分OC, 故①正确;
②∵FB垂直平分OC, ∴△CMB≌△OMB, ∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO, ∴△FOC≌△EOA,
∴FO=EO, 易得OB⊥EF, ∴△OMB≌△OEB, ∴△EOB≌△CMB, 故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE, ∴△BEF是等边三角形, ∴BF=EF,
∵DF∥BE且DF=BE, ∴四边形DEBF是平行四边形, ∴DE=BF, ∴DE=EF, 故③正确;
④在直角△BOE中∵∠3=30°, ∴BE=2OE, ∵∠OAE=∠AOE=30°, ∴AE=OE, ∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2, 故④错误;
所以其中正确结论的个数为3个


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
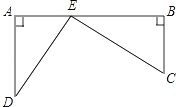
【题目】如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:
(1)在离A站多少km处?
(2)判定三角形DEC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使D′E和C′E重合,折痕是GE,请探索下列问题:
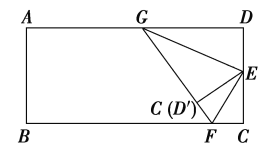
(1)∠FEC′和∠GED′互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些互为余角?哪些互为补角?(各写出两对即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=![]() x+b过点P.
x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
(1)![]() =_______.
=_______.
(2)同理![]() 表示数轴上有理数x所对应的点到-5和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-5和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得![]() =7,这样的整数是_______.
=7,这样的整数是_______.
(3)由以上探索猜想对于任何有理数x,![]() 是否有最小值?如果有,写出最小值;如果没有,说明理由.
是否有最小值?如果有,写出最小值;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长是a,宽是b的长方形硬纸板的四周各剪去一个边长为c的正方形(a>b>2c).再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)若a=12,b=7,c=2,求折合成的长方体盒子的侧面积是多少?
(2)请用含a,b,c的代数式表示折成的长方体盒子的底面周长;
(3)如果把长方体硬纸板的四周剪去2个边长为c的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的底面周长是多少?(用含a,b,c的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com