
【题目】如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使D′E和C′E重合,折痕是GE,请探索下列问题:
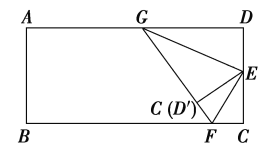
(1)∠FEC′和∠GED′互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些互为余角?哪些互为补角?(各写出两对即可)
【答案】(1)∠FEC′和∠GED′互为余角,理由见解析;(2)∠GEF是直角,理由见解析;(3)见解析.
【解析】
(1)根据翻折的性质可得∠3=∠1,∠4=∠2,然后根据平角等于180°求出∠1+∠2=90°;(2)根据∠GEF=∠1+∠2计算即可得解;(3)根据互余的两个角的和等于90°,互补的两个角的和等于180°分别找出互余和互补的角即可.
(1)如图,由折纸实验,知∠3=∠1,∠4=∠2,而∠1+∠2+∠3+∠4=180°,
所以∠1+∠2=90°,即∠FEC′+∠GED′=90°,
故∠FEC′和∠GED′互为余角.
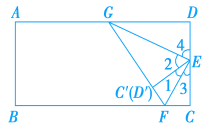
(2)因为∠GEF=∠1+∠2=90°,
所以∠GEF是直角.
(3)∠3和∠4,∠1和∠EFG互为余角,∠AGF和∠DGF,∠CEC′和∠DEC′互为补角(答案不唯一).


科目:初中数学 来源: 题型:
【题目】如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点A1、A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为零的自变量的值称为函数的零点.例如,对于函数y=x-1,令y=0可得x=1,我们就说1是函数y=x-1的零点.
已知y=x2-2mx-2(m+3)(m为常数).
(1)当m=0时,求该函数的零点;
(2)证明:无论m取何值,该函数总有两个零点;
(3)设函数的两个零点分别为x1和x2,且![]() ,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
,此时函数图象与x轴的交点分别为A,B(点A在点B左侧),点M在直线y=x-10上,当MA+MB最小时,求直线AM的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与y轴相交于点A0,过点A0作![]() 轴的平行线交直线y=0.5x+1于点B1,过点 B1作
轴的平行线交直线y=0.5x+1于点B1,过点 B1作![]() 轴的平行线交直线y=x+2于点A1,再过点
轴的平行线交直线y=x+2于点A1,再过点![]() 作
作![]() 轴的平行线交直线y=0.5x+1于点B2,过点 B2作
轴的平行线交直线y=0.5x+1于点B2,过点 B2作![]() 轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )
轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1 ,A2 ,A3 ,…,与直线y=0.5x+1上的点B1,B2,B3,…,则A7B8的长为( )

A.64 B.128 C.256 D.512
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个有理数x,y,z,若x=![]() ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算xy-yn-(y-z)2 014的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com