
����Ŀ��һ���ܱ�13��������Ȼ�����dz�Ϊ��ʮ����������ʮ�������������ǣ����������Ȼ����ĩ��λ��ĩ��λ��ǰ��������ɵ���֮�����ܱ�13��������ô�����Ȼ����һ���ܱ�13���������磺�ж�383357�ܲ��ܱ�13�������������ĩ��λ������357��ĩ��λ��ǰ��������ɵ�����383�����������IJ���383��357=26��26�ܱ�13���������383357����ʮ��������
��1���ж�3253��254514�Ƿ�Ϊ��ʮ����������˵�����ɣ�
��2����һ����λ��Ȼ����ǧλ���ֺ�ʮλ������ͬ����λ�������λ������ͬ����������λ��Ϊ����ͬ������
����֤������һ����λ����ͬ�����ܱ�101������
����һ����λ��Ȼ��������ʮ����������������ͬ������������������������λ�������ֵ����Сֵ֮�
���𰸡���1��3253���ǡ�ʮ��������254514�ǡ�ʮ��������2����֤��������������������������λ�������ֵ����Сֵ֮��Ϊ7878
��������
��1��������Ŀ�С�ʮ�������Ķ�������жϼ��ɣ�
��2���������һ����λ�ġ�ͬ���������ж������101�Ƿ�Ϊ��������֤����
��ͬ�����һ����λ�ġ�ͬ�������ٸ��ݡ�ʮ�������Ķ���ֱ�������ֵ����Сֵ����.
��1���⣺3253���ǡ�ʮ��������254514�ǡ�ʮ���������������£�
��3��253=��250�����ܱ�13������
��3253���ǡ�ʮ��������
��254��514=��260����260��13=��20
��254514�ǡ�ʮ����������3�֣�
��2����֤����������һ����λ����ͬ����Ϊ![]() ��1��a��9��0��b��9��a��bΪ��������
��1��a��9��0��b��9��a��b��������
��![]() =
=![]() =
=![]() =10a+b��
=10a+b��
��a��b������
��10a+b��������
������һ����λ����ͬ�����ܱ�101������
���⣺������һ����λ����ͬ����Ϊ![]() ��1��a��9��0��b��9��a��bΪ��������
��1��a��9��0��b��9��a��b��������
��![]() =
=![]() ����7�֣�
����7�֣�
�������λ��Ȼ���ǡ�ʮ��������
��101b+9a��13�ı�����
��a=1��b=3ʱ��101b+9a=303+9=312��312��13=24����ʱ�����λ����ͬ����Ϊ��1313��
��a=2��b=6ʱ��101b+9a=606+18=624��624��13=48����ʱ�����λ����ͬ����Ϊ��2626��
��a=3��b=9ʱ��101b+9a=909+27=736��936��13=72����ʱ�����λ����ͬ����Ϊ��3939��
��a=5��b=2ʱ��101b+9a=202+45=247��247��13=19����ʱ�����λ����ͬ����Ϊ��5252��
��a=6��b=5ʱ��101b+9a=505+54=559��559��13=43����ʱ�����λ����ͬ����Ϊ��6565��
��a=7��b=8ʱ��101b+9a=808+63=871��871��13=67����ʱ�����λ����ͬ����Ϊ��7878��
��a=9��b=1ʱ��101b+9a=101+81=182��182��13=14����ʱ�����λ����ͬ����Ϊ��9191��
���Ͽ�֪�������λ����ͬ�������Ϊ9191����СΪ1313��
9191��1313=7878��
������������������λ�������ֵ����Сֵ֮��Ϊ7878��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������l1��y=![]() ��x��2��2��2��x��ֱ���O��A���㣬��������l1����ƽ�Ƶõ�l2 �� ����A��AB��x�ύ������l2�ڵ�B�������������l1��l2��ֱ��AB��y����Χ�ɵ���Ӱ���ֵ����Ϊ16����������l2�ĺ�������ʽΪ��������
��x��2��2��2��x��ֱ���O��A���㣬��������l1����ƽ�Ƶõ�l2 �� ����A��AB��x�ύ������l2�ڵ�B�������������l1��l2��ֱ��AB��y����Χ�ɵ���Ӱ���ֵ����Ϊ16����������l2�ĺ�������ʽΪ��������
A.y=![]() ��x��2��2+4
��x��2��2+4
B.y=![]() ��x��2��2+3
��x��2��2+3
C.y=![]() ��x��2��2+2
��x��2��2+2
D.y=![]() ��x��2��2+1
��x��2��2+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
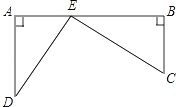
����Ŀ����ͼ����·��A��B�������25km��C��DΪ��ׯ��DA��AB��A��CB��AB��B����֪DA=15km��CB=10km������Ҫ����·AB�Ͻ�һ�����ز�Ʒ�չ�վE��ʹ��C��D���嵽Eվ�ľ�����ȣ��ʣ�
��1������Aվ����km����
��2���ж�������DEC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��E��F�ֱ�Ϊƽ���ı���ABCD��AB��CD���е㣬![]() ��CB���ӳ����ڵ�G��
��CB���ӳ����ڵ�G��
![]() ��֤��
��֤��![]() ��
��![]() ��
��![]() ���ж��ı���DEBF����״����˵�����ɣ�
���ж��ı���DEBF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ����У������Χǽ��һ�Σ�����������Χ��,Χ��һ�����λ�ABCD��ΧǽMN�������25m��.�ּƻ���50m����Χ�����������һ��Χ����ʹ���λ������Ϊ300m2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ѧ����У�С��Ϊ�˲���У�����AB�ĸ߶ȣ�վ�ڽ�ѧ¥�ϵ�C�������˵Ͷ�B�ĸ���Ϊ45�㣬�����˶���A������Ϊ30�㣬��������ѧ¥��ˮƽ����CDΪ9m������˵ĸ߶��Ƕ��٣�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ҵ�������ֽ�Ŀ�DC���е�E������C��E����������һ���ǣ��ۺ���EF���ٽ���D��E������ʹD��E��C��E�غϣ��ۺ���GE����̽���������⣺
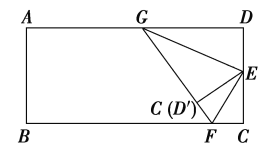
(1)��FEC���͡�GED����Ϊ�����Ϊʲô��
(2)��GEF��ֱ����Ϊʲô��
(3)��������ֽͼ���У�������Щ��Ϊ��ǣ���Щ��Ϊ���ǣ�(��д�����Լ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ�ʽ���� ![]() �⣬��m��ֵΪ��������
�⣬��m��ֵΪ��������
A.��1.5
B.1
C.��1.5��2
D.��0.5��1.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų���a������b�ij�����Ӳֽ������ܸ���ȥһ���߳�Ϊc�������Σ�a��b��2c�������ۺϳ�һ���ǵij�������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ���
��1����a=12��b=7��c=2�����ۺϳɵij�������ӵIJ�����Ƕ��٣�
��2�����ú�a��b��c�Ĵ���ʽ��ʾ�۳ɵij�������ӵĵ����ܳ���
��3������ѳ�����Ӳֽ������ܼ�ȥ2���߳�Ϊc�������κ�2��ͬ����״��ͬ����С�ij����Σ�Ȼ���ۺϳ�һ���иǵij�������ӣ���ô���ĵ����ܳ��Ƕ��٣����ú�a��b��c�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com