
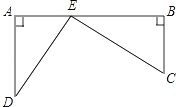
【题目】如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:
(1)在离A站多少km处?
(2)判定三角形DEC的形状.
科目:初中数学 来源: 题型:
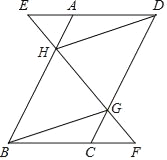
【题目】已知:如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点H,G,连接DH,BG.
(1)求证:△AEH≌△CFG;
(2)连接BE,若BE=DE,则四边形BGDH是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3,BC=5,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F.
(1)求证:四边形CEDF是平行四边形;
(2)① 当AE= 时,四边形CEDF是矩形;
② 当AE= 时,四边形CEDF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式
(1)﹣(﹣5)﹣(+7)
(2)|﹣5﹣8|+24÷(﹣3)
(3)﹣0.25÷(﹣![]() )×(1﹣
)×(1﹣![]() )
)
(4)36×(![]() )
)
(5)1÷[![]() ﹣(﹣1+1
﹣(﹣1+1![]() )]×4
)]×4
(6)23﹣(1﹣0.5)×![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点A1、A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com