
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
【答案】证明:(1)连接AC,
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°﹣∠B=120°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∵∠AEF=60°,
∴∠FEC=90°﹣∠AEF=30°,
∴∠CFE=180°﹣∠FEC﹣∠ECF=180°﹣30°﹣120°=30°,
∴∠FEC=∠CFE,
∴EC=CF,
∴BE=DF;
(2)∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,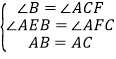
∴△ABE≌△ACF(AAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形.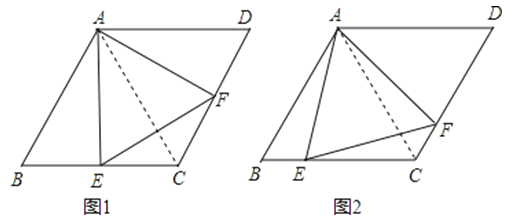
【解析】(1)首先连接AC,由菱形ABCD中,∠B=60°,根据菱形的性质,易得△ABC是等边三角形,又由三线合一,可证得AE⊥BC,继而求得∠FEC=∠CFE,即可得EC=CF,继而证得BE=DF;
(2)首先由△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得:△AEF是等边三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点A1、A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3个有理数x,y,z,若x=![]() ,且x与y互为相反数,y是z的倒数.
,且x与y互为相反数,y是z的倒数.
(1)当n为奇数时,你能求出x,y,z这三个数吗?当n为偶数时,你能求出x,y,z这三个数吗?若能,请计算并写出结果;若不能,请说明理由.
(2)根据(1)的结果计算xy-yn-(y-z)2 014的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 筐葡萄,以每筐
筐葡萄,以每筐![]() 千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
单位(千克) |
|
|
|
|
|
|
筐数 |
|
|
|
|
|
|
(1)![]() 筐葡萄中,最重的一筐比最轻的一筐重________千克.
筐葡萄中,最重的一筐比最轻的一筐重________千克.
(2)与标准重量比较,![]() 筐葡萄总计超过或不足多少千克?
筐葡萄总计超过或不足多少千克?
(3)若葡萄每千克售价![]() 元,则出售这
元,则出售这![]() 筐葡萄可卖多少元?
筐葡萄可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
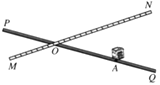
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为()
A. ![]() 秒 B. 16秒 C.
秒 B. 16秒 C. ![]() 秒 D. 24秒
秒 D. 24秒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com