
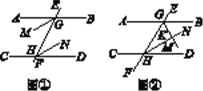
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

【答案】 (1)GM∥HN.理由见解析;(2)(1)中的结论仍然成立.理由见解析;(3)(1)中的结论不成立.结论:GM⊥HN,理由见解析.
【解析】试题分析:(1)根据平行线的性质可得![]() ,根据角平分线的性质可得
,根据角平分线的性质可得![]() 和
和![]() 的关系,进而
的关系,进而![]() 和
和![]() 的关系,再根据平行线的判定可得
的关系,再根据平行线的判定可得![]() 和
和![]() 的位置关系;
的位置关系;
(2)画出图形,同理根据平行线的性质可得![]() 和
和![]() 的关系,根据角平分线的定义和等量代换可得
的关系,根据角平分线的定义和等量代换可得![]() 再根据平行线的判定可得
再根据平行线的判定可得![]() 和
和![]() 的位置关系;
的位置关系;
(3)画出图形,根据两直线平行,同旁内角互补可得![]() 和
和![]() 的关系,根据角平分线的定义和等量代换可求得
的关系,根据角平分线的定义和等量代换可求得![]() 至此得到结论.
至此得到结论.
试题解析: (1)GM∥HN.
理由:∵AB∥CD, ![]()
∵GM,HN分别为∠BGE和∠DHG的平分线,
∴![]()
∴![]()
∴GM∥HN.
(2)(1)中的结论仍然成立.
理由:如图①,∵AB∥CD,
∴![]()
∵GM,HN分别为∠AGH和∠DHG的平分线,
∴![]()
∴![]()
∴GM∥HN.
(3)(1)中的结论不成立.
结论: ![]()
理由:如图②,∵AB∥CD,∴![]()
∵GM,HN分别为∠BGH和∠DHG的平分线,
∴![]()
∴![]()
设GM,HN相交于点K, ![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,其余三面用围栏,围成一个矩形花园ABCD(围墙MN最长可利用25m).现计划用50m长的围栏,请你设计一种围法,使矩形花园的面积为300m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线l1上一点,另一直线l2:y2=![]() x+b过点P.
x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线l2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.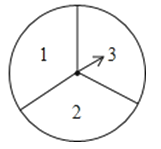
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长是a,宽是b的长方形硬纸板的四周各剪去一个边长为c的正方形(a>b>2c).再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)若a=12,b=7,c=2,求折合成的长方体盒子的侧面积是多少?
(2)请用含a,b,c的代数式表示折成的长方体盒子的底面周长;
(3)如果把长方体硬纸板的四周剪去2个边长为c的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的底面周长是多少?(用含a,b,c的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯长AB=6m,∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图所示).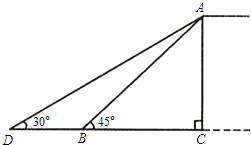
(结果保留根号)
(1)求调整后楼梯AD的长;
(2)求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
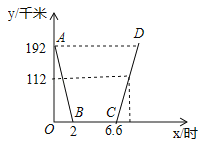
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在一次函数图象上的位置如图所示,两点的坐标分别为A(x+a,y+b),B(x,y),下列结论正确的是( )
A.a>0
B.a<0
C.b=0
D.ab<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com