
【题目】如图,正方形ABCD中,E为DC边上一点,且DE=1,AE=EF,∠AEF=90°,则FC= ( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 
(1)如图1,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D.
(2)如图2,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上. ①求sinB的值;
②画出△ABC关于直线l对称的△A1B1C1(A与A1 , B与B1 , C与C1相对应),连接AA1 , BB1 , 并计算梯形AA1B1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为()
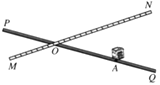
A. ![]() 秒 B. 16秒 C.
秒 B. 16秒 C. ![]() 秒 D. 24秒
秒 D. 24秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE= ![]()

(1)求证:BC是⊙O的切线;
(2)求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1 , a2 , …,a2017是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,则a1 , a2 , …,a2017中为0的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com